In the children’s book “One Grain of Rice: A Mathematical Folktale” a girl uses her knowledge of exponential growth to trick a greedy king into turning over his stockpile of rice. Hidden in the story are mathematical concepts related to doubling: powers of two, geometric sequences, geometric series, and exponents. I will analyze the story from this perspective, and then discuss my experience reading it to first and third grade students.

Synopsis
In the story, a girl named Rani is given an amount of rice each day for thirty days: one grain of rice on day one, two grains of rice on day two, four grains of rice on day three, eight grains of rice on day four, etc. In other words, on each day after the first, she receives double the amount of rice she received on the previous day. Since the doubling starts from one grain of rice, the amounts received correspond to the first 30 nonnegative powers of two.
The story progresses through select days, describing the number of grains received, the capacity and number of containers used to hold them, and the total received to each point. The amounts of each measure of rice are not spelled out for each day, so I filled in the details.
Containers
To manage the description of the number of grains of rice, and to put the growth in perspective, the author (Demi) uses these containers: bowls, bags, baskets, and storehouses:
- 1 bowl = 4,096 grains
- 1 bag = 8 bowls = 32,768 grains
- 1 basket = 32 bags = 256 bowls = 1,048,576 grains
- 1 storehouse = 128 baskets = 4,096 bags = 32,768 bowls = 134,217,728 grains
(I inferred some of these relationships from the story.)
The units of the containers themselves progress through powers of two — not only through nonnegative powers of two, but through negative powers of two as well. Nonnegative powers of two represent whole number units, and negative powers of two represent fractional units. For example, 1,024 grains of rice is 1/4 of a bowl and 2,048 grains is 1/2 a bowl.
A sequence of powers of two is a geometric sequence, also known as a geometric progression; in this case, each number in the sequence is double the previous.
Rice Received, By Day
I made a table showing the progression of powers of two by day, by measure; negative powers of two amounts are shown in gray (I generated this table, and the ones that follow, with PARI/GP scripts I wrote):
| Day | Grains | Bowls | Bags | Baskets | Storehouses |
|---|---|---|---|---|---|
| 1 | 1 | 1/4096 | 1/32768 | 1/1048576 | 1/134217728 |
| 2 | 2 | 1/2048 | 1/16384 | 1/524288 | 1/67108864 |
| 3 | 4 | 1/1024 | 1/8192 | 1/262144 | 1/33554432 |
| 4 | 8 | 1/512 | 1/4096 | 1/131072 | 1/16777216 |
| 5 | 16 | 1/256 | 1/2048 | 1/65536 | 1/8388608 |
| 6 | 32 | 1/128 | 1/1024 | 1/32768 | 1/4194304 |
| 7 | 64 | 1/64 | 1/512 | 1/16384 | 1/2097152 |
| 8 | 128 | 1/32 | 1/256 | 1/8192 | 1/1048576 |
| 9 | 256 | 1/16 | 1/128 | 1/4096 | 1/524288 |
| 10 | 512 | 1/8 | 1/64 | 1/2048 | 1/262144 |
| 11 | 1024 | 1/4 | 1/32 | 1/1024 | 1/131072 |
| 12 | 2048 | 1/2 | 1/16 | 1/512 | 1/65536 |
| 13 | 4096 | 1 | 1/8 | 1/256 | 1/32768 |
| 14 | 8192 | 2 | 1/4 | 1/128 | 1/16384 |
| 15 | 16384 | 4 | 1/2 | 1/64 | 1/8192 |
| 16 | 32768 | 8 | 1 | 1/32 | 1/4096 |
| 17 | 65536 | 16 | 2 | 1/16 | 1/2048 |
| 18 | 131072 | 32 | 4 | 1/8 | 1/1024 |
| 19 | 262144 | 64 | 8 | 1/4 | 1/512 |
| 20 | 524288 | 128 | 16 | 1/2 | 1/256 |
| 21 | 1048576 | 256 | 32 | 1 | 1/128 |
| 22 | 2097152 | 512 | 64 | 2 | 1/64 |
| 23 | 4194304 | 1024 | 128 | 4 | 1/32 |
| 24 | 8388608 | 2048 | 256 | 8 | 1/16 |
| 25 | 16777216 | 4096 | 512 | 16 | 1/8 |
| 26 | 33554432 | 8192 | 1024 | 32 | 1/4 |
| 27 | 67108864 | 16384 | 2048 | 64 | 1/2 |
| 28 | 134217728 | 32768 | 4096 | 128 | 1 |
| 29 | 268435456 | 65536 | 8192 | 256 | 2 |
| 30 | 536870912 | 131072 | 16384 | 512 | 4 |
(The thirteen days mentioned explicitly in the story are shown in bold).
Here’s the same table, but using exponents to make the powers of two progressions more obvious:
| Day | Grains | Bowls | Bags | Baskets | Storehouses |
|---|---|---|---|---|---|
| 1 | 20 | 2-12 | 2-15 | 2-20 | 2-27 |
| 2 | 21 | 2-11 | 2-14 | 2-19 | 2-26 |
| 3 | 22 | 2-10 | 2-13 | 2-18 | 2-25 |
| 4 | 23 | 2-9 | 2-12 | 2-17 | 2-24 |
| 5 | 24 | 2-8 | 2-11 | 2-16 | 2-23 |
| 6 | 25 | 2-7 | 2-10 | 2-15 | 2-22 |
| 7 | 26 | 2-6 | 2-9 | 2-14 | 2-21 |
| 8 | 27 | 2-5 | 2-8 | 2-13 | 2-20 |
| 9 | 28 | 2-4 | 2-7 | 2-12 | 2-19 |
| 10 | 29 | 2-3 | 2-6 | 2-11 | 2-18 |
| 11 | 210 | 2-2 | 2-5 | 2-10 | 2-17 |
| 12 | 211 | 2-1 | 2-4 | 2-9 | 2-16 |
| 13 | 212 | 20 | 2-3 | 2-8 | 2-15 |
| 14 | 213 | 21 | 2-2 | 2-7 | 2-14 |
| 15 | 214 | 22 | 2-1 | 2-6 | 2-13 |
| 16 | 215 | 23 | 20 | 2-5 | 2-12 |
| 17 | 216 | 24 | 21 | 2-4 | 2-11 |
| 18 | 217 | 25 | 22 | 2-3 | 2-10 |
| 19 | 218 | 26 | 23 | 2-2 | 2-9 |
| 20 | 219 | 27 | 24 | 2-1 | 2-8 |
| 21 | 220 | 28 | 25 | 20 | 2-7 |
| 22 | 221 | 29 | 26 | 21 | 2-6 |
| 23 | 222 | 210 | 27 | 22 | 2-5 |
| 24 | 223 | 211 | 28 | 23 | 2-4 |
| 25 | 224 | 212 | 29 | 24 | 2-3 |
| 26 | 225 | 213 | 210 | 25 | 2-2 |
| 27 | 226 | 214 | 211 | 26 | 2-1 |
| 28 | 227 | 215 | 212 | 27 | 20 |
| 29 | 228 | 216 | 213 | 28 | 21 |
| 30 | 229 | 217 | 214 | 29 | 22 |
Finally, here’s the same information, condensed into simple formulas:
- Number of grains on day d = 2d-1
- Number of bowls on day d = 2d-13
- Number of bags on day d = 2d-16
- Number of baskets on day d = 2d-21
- Number of storehouses on day d = 2d-28
These relationships are simple: each measure doubles each day, so the exponent of each power of two increases by one each day. The offset in the exponent of the container formulas shows where each transitions from negative powers of two to nonnegative powers of two.
Cumulative Rice Received, By Day
I made a table showing the cumulative number of grains of rice by day, by measure. The amounts are not powers of two, although they follow a pattern, which I’ll explain below. The table is broken into two parts (to fit on this page), with fractional amounts less than one shown in gray:
| Day | Grains | Bowls | Bags |
|---|---|---|---|
| 1 | 1 | 1/4096 | 1/32768 |
| 2 | 3 | 3/4096 | 3/32768 |
| 3 | 7 | 7/4096 | 7/32768 |
| 4 | 15 | 15/4096 | 15/32768 |
| 5 | 31 | 31/4096 | 31/32768 |
| 6 | 63 | 63/4096 | 63/32768 |
| 7 | 127 | 127/4096 | 127/32768 |
| 8 | 255 | 255/4096 | 255/32768 |
| 9 | 511 | 511/4096 | 511/32768 |
| 10 | 1023 | 1023/4096 | 1023/32768 |
| 11 | 2047 | 2047/4096 | 2047/32768 |
| 12 | 4095 | 4095/4096 | 4095/32768 |
| 13 | 8191 | 1 4095/4096 | 8191/32768 |
| 14 | 16383 | 3 4095/4096 | 16383/32768 |
| 15 | 32767 | 7 4095/4096 | 32767/32768 |
| 16 | 65535 | 15 4095/4096 | 1 32767/32768 |
| 17 | 131071 | 31 4095/4096 | 3 32767/32768 |
| 18 | 262143 | 63 4095/4096 | 7 32767/32768 |
| 19 | 524287 | 127 4095/4096 | 15 32767/32768 |
| 20 | 1048575 | 255 4095/4096 | 31 32767/32768 |
| 21 | 2097151 | 511 4095/4096 | 63 32767/32768 |
| 22 | 4194303 | 1023 4095/4096 | 127 32767/32768 |
| 23 | 8388607 | 2047 4095/4096 | 255 32767/32768 |
| 24 | 16777215 | 4095 4095/4096 | 511 32767/32768 |
| 25 | 33554431 | 8191 4095/4096 | 1023 32767/32768 |
| 26 | 67108863 | 16383 4095/4096 | 2047 32767/32768 |
| 27 | 134217727 | 32767 4095/4096 | 4095 32767/32768 |
| 28 | 268435455 | 65535 4095/4096 | 8191 32767/32768 |
| 29 | 536870911 | 131071 4095/4096 | 16383 32767/32768 |
| 30 | 1073741823 | 262143 4095/4096 | 32767 32767/32768 |
| Day | Grains | Baskets | Storehouses |
|---|---|---|---|
| 1 | 1 | 1/1048576 | 1/134217728 |
| 2 | 3 | 3/1048576 | 3/134217728 |
| 3 | 7 | 7/1048576 | 7/134217728 |
| 4 | 15 | 15/1048576 | 15/134217728 |
| 5 | 31 | 31/1048576 | 31/134217728 |
| 6 | 63 | 63/1048576 | 63/134217728 |
| 7 | 127 | 127/1048576 | 127/134217728 |
| 8 | 255 | 255/1048576 | 255/134217728 |
| 9 | 511 | 511/1048576 | 511/134217728 |
| 10 | 1023 | 1023/1048576 | 1023/134217728 |
| 11 | 2047 | 2047/1048576 | 2047/134217728 |
| 12 | 4095 | 4095/1048576 | 4095/134217728 |
| 13 | 8191 | 8191/1048576 | 8191/134217728 |
| 14 | 16383 | 16383/1048576 | 16383/134217728 |
| 15 | 32767 | 32767/1048576 | 32767/134217728 |
| 16 | 65535 | 65535/1048576 | 65535/134217728 |
| 17 | 131071 | 131071/1048576 | 131071/134217728 |
| 18 | 262143 | 262143/1048576 | 262143/134217728 |
| 19 | 524287 | 524287/1048576 | 524287/134217728 |
| 20 | 1048575 | 1048575/1048576 | 1048575/134217728 |
| 21 | 2097151 | 1 1048575/1048576 | 2097151/134217728 |
| 22 | 4194303 | 3 1048575/1048576 | 4194303/134217728 |
| 23 | 8388607 | 7 1048575/1048576 | 8388607/134217728 |
| 24 | 16777215 | 15 1048575/1048576 | 16777215/134217728 |
| 25 | 33554431 | 31 1048575/1048576 | 33554431/134217728 |
| 26 | 67108863 | 63 1048575/1048576 | 67108863/134217728 |
| 27 | 134217727 | 127 1048575/1048576 | 134217727/134217728 |
| 28 | 268435455 | 255 1048575/1048576 | 1 134217727/134217728 |
| 29 | 536870911 | 511 1048575/1048576 | 3 134217727/134217728 |
| 30 | 1073741823 | 1023 1048575/1048576 | 7 134217727/134217728 |
The pattern is easier to see if you rewrite the values using exponents, and write mixed numbers as improper fractions:
| Day | Grains | Bowls | Bags | Baskets | Storehouses |
|---|---|---|---|---|---|
| 1 | 21 – 1 | (21 – 1)/212 | (21 – 1)/215 | (21 – 1)/220 | (21 – 1)/227 |
| 2 | 22 – 1 | (22 – 1)/212 | (22 – 1)/215 | (22 – 1)/220 | (22 – 1)/227 |
| 3 | 23 – 1 | (23 – 1)/212 | (23 – 1)/215 | (23 – 1)/220 | (23 – 1)/227 |
| 4 | 24 – 1 | (24 – 1)/212 | (24 – 1)/215 | (24 – 1)/220 | (24 – 1)/227 |
| 5 | 25 – 1 | (25 – 1)/212 | (25 – 1)/215 | (25 – 1)/220 | (25 – 1)/227 |
| 6 | 26 – 1 | (26 – 1)/212 | (26 – 1)/215 | (26 – 1)/220 | (26 – 1)/227 |
| 7 | 27 – 1 | (27 – 1)/212 | (27 – 1)/215 | (27 – 1)/220 | (27 – 1)/227 |
| 8 | 28 – 1 | (28 – 1)/212 | (28 – 1)/215 | (28 – 1)/220 | (28 – 1)/227 |
| 9 | 29 – 1 | (29 – 1)/212 | (29 – 1)/215 | (29 – 1)/220 | (29 – 1)/227 |
| 10 | 210 – 1 | (210 – 1)/212 | (210 – 1)/215 | (210 – 1)/220 | (210 – 1)/227 |
| 11 | 211 – 1 | (211 – 1)/212 | (211 – 1)/215 | (211 – 1)/220 | (211 – 1)/227 |
| 12 | 212 – 1 | (212 – 1)/212 | (212 – 1)/215 | (212 – 1)/220 | (212 – 1)/227 |
| 13 | 213 – 1 | (213 – 1)/212 | (213 – 1)/215 | (213 – 1)/220 | (213 – 1)/227 |
| 14 | 214 – 1 | (214 – 1)/212 | (214 – 1)/215 | (214 – 1)/220 | (214 – 1)/227 |
| 15 | 215 – 1 | (215 – 1)/212 | (215 – 1)/215 | (215 – 1)/220 | (215 – 1)/227 |
| 16 | 216 – 1 | (216 – 1)/212 | (216 – 1)/215 | (216 – 1)/220 | (216 – 1)/227 |
| 17 | 217 – 1 | (217 – 1)/212 | (217 – 1)/215 | (217 – 1)/220 | (217 – 1)/227 |
| 18 | 218 – 1 | (218 – 1)/212 | (218 – 1)/215 | (218 – 1)/220 | (218 – 1)/227 |
| 19 | 219 – 1 | (219 – 1)/212 | (219 – 1)/215 | (219 – 1)/220 | (219 – 1)/227 |
| 20 | 220 – 1 | (220 – 1)/212 | (220 – 1)/215 | (220 – 1)/220 | (220 – 1)/227 |
| 21 | 221 – 1 | (221 – 1)/212 | (221 – 1)/215 | (221 – 1)/220 | (221 – 1)/227 |
| 22 | 222 – 1 | (222 – 1)/212 | (222 – 1)/215 | (222 – 1)/220 | (222 – 1)/227 |
| 23 | 223 – 1 | (223 – 1)/212 | (223 – 1)/215 | (223 – 1)/220 | (223 – 1)/227 |
| 24 | 224 – 1 | (224 – 1)/212 | (224 – 1)/215 | (224 – 1)/220 | (224 – 1)/227 |
| 25 | 225 – 1 | (225 – 1)/212 | (225 – 1)/215 | (225 – 1)/220 | (225 – 1)/227 |
| 26 | 226 – 1 | (226 – 1)/212 | (226 – 1)/215 | (226 – 1)/220 | (226 – 1)/227 |
| 27 | 227 – 1 | (227 – 1)/212 | (227 – 1)/215 | (227 – 1)/220 | (227 – 1)/227 |
| 28 | 228 – 1 | (228 – 1)/212 | (228 – 1)/215 | (228 – 1)/220 | (228 – 1)/227 |
| 29 | 229 – 1 | (229 – 1)/212 | (229 – 1)/215 | (229 – 1)/220 | (229 – 1)/227 |
| 30 | 230 – 1 | (230 – 1)/212 | (230 – 1)/215 | (230 – 1)/220 | (230 – 1)/227 |
Each value is simply the number of grains of rice accumulated, divided by the size of the corresponding measure in grains:
- Number of grains through day d: 2d – 1
- Number of bowls through day d: (2d – 1)/212
- Number of bags through day d: (2d – 1)/215
- Number of baskets through day d: (2d – 1)/220
- Number of storehouses through day d: (2d – 1)/227
The sum of grains is a geometric series, being the sum of numbers from a geometric sequence — in this case, the first d nonnegative powers of two. Conveniently, we don’t need to add them to know their total; this well-known formula gives their sum directly:
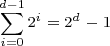
(Numbers of the form 2n – 1 are called Mersenne numbers.)
For example, on day 15, 215 – 1 = 32767 grains of rice have accumulated, an amount that would fill (215 – 1)/212 = 32767/4096 = 7 4095/4096 bowls.
The Formulas for Representation as Mixed Numbers
The simple formulas above, expressed as improper fractions, hide the pattern that lies in the mixed number representation of the values of the containers.
Each value is a sum of consecutive powers of two. Some values are sums of negative powers of two, and some are sums of both negative and nonnegative powers of two. Values for measures that start out accumulating in fractional units (each measure except grains) are sums of negative powers of two. At some point, when whole number units start to add in, sums of nonnegative powers of two become part of the total. This is when the value becomes an improper fraction, or mixed number.
These formulas take into account the point at which the values become improper fractions, but expressing them as mixed numbers:
- Number of bowls through day d:
If day ≤ 12: (2d – 1)/212
If day > 12: (2d-12 – 1) + (212 – 1)/212 - Number of bags through day d:
If day ≤ 15: (2d – 1)/215
If day > 15: (2d-15 – 1) + (215 – 1)/215 - Number of baskets through day d:
If day ≤ 20: (2d – 1)/220
If day > 20: (2d-20 – 1) + (220 – 1)/220 - Number of storehouses through day d:
If day ≤ 27: (2d – 1)/227
If day > 27: (2d-27 – 1) + (227 – 1)/227
Fractional values accumulate as a Mersenne number over a power of two; once whole number values begin to add in, the accumulated fractional part remains unchanged while the whole number part accumulates as a Mersenne number.
It’s easy to show that the mixed number formulas are equivalent to the improper fraction formulas. For example, take the mixed number formula for bowls after day 12:

You can rewrite this, using simple algebra and the laws of exponents, as follows:
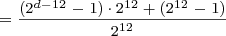
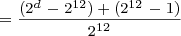

This is the same formula as for before day 12, and thus the same formula for all days.
In the Classroom
This is a good story upon which to base a math lesson, and you can vary the mathematical sophistication according to grade level. I read it to first and third graders, so I had to keep it simple. My goal was to show how numbers grow through doubling, and to introduce place value of large numbers.
First Graders
When I read the story to a first grade class, I got lots of “oohs” and “aahs” whenever I read a big number from the text and whenever they saw an illustration of the many animals needed to transport the rice. At the end of the story, I wrote 1,073,741,823 on the board to show them how it looks in numerals. Although I knew they’d only been taught up to the hundreds place, I went through each place and named it. I finished by saying “when you get to third grade I can explain the math a little more.”
Third Graders
For the third grade class, I read the story and spent about fifteen minutes afterwards discussing the numbers. First I wrote 1,073,741,823 on the board and went through the places. Even though they had been taught only up to the thousands place, most of them knew to the billions place (and beyond). Next, I asked them to say the number in words, and many had difficulty — particularly the “seven-hundred forty one thousand” part (I don’t know why it was harder than “seventy-three million” — I would have thought the zero in the hundred millions place would be confusing).
Next, I wrote the number 1 and had them tell me the next numbers in the sequence. A couple of kids answered correctly up to 8,192 (214). When I asked one boy if he had them memorized, he said “No, I can add them in my head.”
I continued the sequence using a pocket calculator. I had the students take turns computing the next number with it (they found it very hard to recite the numbers back to me, because there were no commas). By design, one unlucky kid had 227 (134,217,728) for his turn, which caused the calculator to overflow. I told the class that the numbers get so big that you need a computer to figure them out.
At the end, I referred to these numbers as “powers of two,” and told them they would be useful someday if they wanted to work with computers (can you blame me for plugging my profession?).
One boy asked a good question: “what if you got 20 grains every minute for 30 days — would that be more?” I said “Great question: I think you’d still get more by doubling though.” The calculator showed him this to be true — his method accumulated only 864,000 grains.
Lesson Plan Resources
If you search the Internet for “One Grain of Rice” you’ll find other ideas on how to incorporate this story into a math lesson. For example, this worksheet uses graphs and logarithms.
Errors in the Story
I found two errors and one inconsistency in the story:
Before the Rice Is Delivered
Rani describes her plan for receiving the rice as follows:
“Today, you will give me a single grain of rice. Then, each day for thirty days you will give me double the rice you gave me the day before. Thus, tomorrow you will give me two grains of rice, the next day four grains of rice, and so on for thirty days.”
The doubling occurs for twenty-nine days, not thirty days.
On Day 16
On day 16 it says
“On the sixteenth day, Rani was presented with a bag containing thirty-two thousand, seven hundred and sixty-eight grains of rice. All together she had enough rice for two full bags”
Through day 16 she had 65,535 grains of rice, one grain less than two full bags; she actually had 1 32767/32768 = 1.999969482421875 bags.
On Day 9
On day 9 it says
“On the ninth day, Rani was presented with two hundred and fifty-six grains of rice. She had received in all five hundred and eleven grains of rice, only enough for a small handful.”
Technically, there’s nothing wrong with this, but the measure “small handful” — 511 grains — is not a power of two. It doesn’t fit neatly into the scheme of other units (and hence is why I didn’t include it in the tables).

Wow…excellent analysis!
Can’t wait for 1073741823 comments for this one!
Visiting the UN I learned about the Web site freerice.com. As of 5/5/16 over 97 billion grains of rice have been donated. That total is equivalent to between 36 (236 = 68,719,476,735) and 37 (237 = 137,438,953,471) days according to our daily doubling scheme.