Nines in Quinary

In my article “Nines in Binary”, I proved the following: positive integers of the form 10ⁿ-1, that is, integers made up of n digits of 9s, have binary representations with exactly n digits of trailing 1s. Pat Ballew made a clever observation, adapting my result to prove an equivalent statement for base 5 (quinary): positive integers of the form 10ⁿ-1 have quinary representations that have exactly n digits of trailing 4s. For example, 9999 in decimal is 304444 in quinary.

In “Nines in Binary”, I derived an expression for 10ⁿ – 1 that shows its structure as a binary number:

10ⁿ – 1 = (5ⁿ – 1) 2ⁿ + (2ⁿ – 1)

Pat derived a similar expression for 10ⁿ – 1 that shows its structure as a quinary number:

10ⁿ – 1 = (2ⁿ – 1) 5ⁿ + (5ⁿ – 1)

In essence, he swapped the 2s and 5s, making it the “dual” of my formula, if you will.

I’ll show the details of the derivation and prove why the formula works.

Deriving the Expression

To derive the formula for the “binary expression” of 10ⁿ – 1, I worked backwards from the patterns I saw in its binary representation:

(5ⁿ – 1) 2ⁿ + (2ⁿ – 1) = 5ⁿ2ⁿ – 2ⁿ + 2ⁿ – 1 = 10ⁿ – 1

Pat derived the formula for the “quinary expression” of 10ⁿ – 1 without having to look at its representation in quinary — he simply modified the algebra that I presented. He observed that – 2ⁿ + 2ⁿ could be replaced with – 5ⁿ + 5ⁿ, since both equal 0. This allowed him to rearrange the expression as follows:

10ⁿ – 1 = 2ⁿ5ⁿ – 5ⁿ + 5ⁿ – 1 = (2ⁿ – 1) 5ⁿ + (5ⁿ – 1)

What the Expression Shows

The quinary expression has a leading part, 2ⁿ – 1 shifted left n places in base 5, and a trailing part, 5ⁿ – 1. The trailing part shows that there are at least n trailing 4s, since 5ⁿ – 1 is n 4s in quinary (like 2ⁿ – 1 is n 1s in binary, 10ⁿ – 1 is n 9s in decimal, etc.). The leading part shows that there are exactly n trailing 4s, since 2ⁿ – 1 does not end with the digit 4 in quinary. Let’s see why.

To show that 2ⁿ – 1, when expressed in base 5, does not end in 4, we can use modular arithmetic. Let’s start by analyzing the possible ending digits of the positive powers of two:

• 
• 
• 
• 
• 
• …

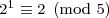
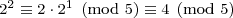
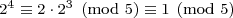
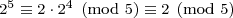
This shows the numbers 2ⁿ (n ≥ 1) mod 5 cycle through the ending digits 2, 4, 3, and 1. This means that the numbers 2ⁿ – 1 cycle through the ending digits 1, 3, 2, and 0. The digit 4 is not on the list!

Nonnegative Powers of Ten in Quinary

In my article “A Pattern in Powers of Ten and Their Binary Equivalents”, I showed that the trailing digits of nonnegative powers of ten, in binary, match the power of ten; in other words, a 1 is followed by n trailing 0s. For example, 100₁₀ = 1100100₂.

A similar, though slightly weaker property, holds for nonnegative powers of ten in quinary: 10ⁿ ends with n 0s. A nonnegative power of ten is a multiple of a power of two and a power of five: 10ⁿ = 2ⁿ * 5ⁿ. A power of two in base 5 ends in 1, 2, 3, or 4 — never 0 — as I showed above. When you multiply a power of two by a power of five, you shift the power of two left by n places in base 5, which adds n trailing 0s. So the quinary representation ends with a nonzero digit followed by n 0s — exactly n trailing 0s!