“0.1 Repeating” In Binary Equals 1

In decimal, “0.9 repeating”, or 0.9, equals 1. In binary, a similar thing is true: “0.1 repeating”, or 0.1, equals 1. I’ll show you three ways to prove it, using the three bicimal to fraction conversion algorithms I described recently.

Proof Using the Series Method

A repeating bicimal is really an infinite geometric series, so one way to prove 0.1 = 1 is to use the series method:

0.1 = 0.111…

= 0.1 + 0.01 + 0.001 + …

= 1/10 + 1/100 + 1/1000 + …

= 1/2 + 1/4 + 1/8 + … (converting to decimal numerals makes it easier)

= 1/2¹ + 1/2² + 1/2³ + …

= (1/2)¹ + (1/2)² + (1/2)³ + …

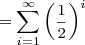
$\mbox{\footnotesize{\displaystyle = \sum_{i=1}^\infty \left(\frac{1}{2}\right)^{i}}}$

As I showed when I described the series method, that summation resolves to the formula

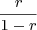$\mbox{\footnotesize{\displaystyle \frac{r}{1-r}}}}$ ,

where r = 1/2 in this case:

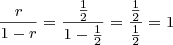
$\mbox{\footnotesize{\displaystyle \frac{r}{1-r} = \frac{\frac{1}{2}}{1-\frac{1}{2}} = \frac{\frac{1}{2}}{\frac{1}{2}} = 1}}}$

What Did We Prove Exactly?

This proof convinces you only inasmuch as you accept the proof of the formula for infinite geometric series. It’s a tough thing to accept at first — infinity is a strange concept. You have to think of the series as a fixed sum, not as a never-ending process of adding tinier and tinier numbers that gets you ever so close to — but never equal to — 1.

Proof Using the Subtraction Method

You can also prove 0.1 = 1 using the subtraction method:

b = 0.1

10b = 1.1

10b – b = 1

b = 1

(All numerals are in binary.)

Look at that: b started out as 0.1 and ended up as 1; it’s 0.1 and 1 at the same time!

What Did We Prove Exactly?

This looks like mathematical sleight of hand. We shifted the bicimal left, yet the fractional part remained unchanged. And we subtracted an infinite string of 1s from an infinite string of 1s — is that legal? In the land of infinity, this is OK.

Proof Using the Direct Method

You can prove 0.1 = 1 using the direct method, which is really just a distillation of the series and subtraction methods. The direct method says to treat the repeating portion as an integer, and to place that integer over a denominator consisting of as many 1s as there are digits in the repeating portion. 0.1 is a pure repeating bicimal with a repeating cycle of one digit, so the fraction it converts to is 1/1; in other words, 1.

Discussion

In binary, 0.1 is another name for 1. Similar dual naming exists for all bicimals: just as decimal 0.29 = 0.3 and 0.1589 = 0.159, binary 0.01 = 0.1 and 0.10101 = 0.1011. The trailing repeating 1s are the same as a 1 in the next higher place. You can show this using the same three methods above.