A Standard Definition of The Powers of Two

What is a power of two exactly? Is 2⁰ a power of two? Is 2^-1 a power of two? How about 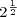or ? It depends on how you define it; there are several definitions from which you could choose. Let’s see if we can sort them out and propose a standard definition, or at least a standard definition for our use.

Let’s start with the easy part: 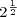and , although in form look like powers of two, are not commonly referred to as such. To include noninteger exponents would make for a very uninteresting definition, most certainly in the case of irrational exponents; that would make every positive real number a power of two (think about the curve y = 2^x)! We will stick with convention and keep the definition useful by considering only integer exponents.

So back to 2⁰ and 2^-1 — are they powers of two? It depends on which of the following three commonly used definitions you subscribe to:

1. The powers of two = {2ⁿ | n is an integer > 0}.
2. The powers of two = {2ⁿ | n is an integer ≥ 0}.
3. The powers of two = {2ⁿ | n is an integer}.

Definition 1 describes a subset of definition 2, which in turn describes a subset of definition 3. Under definition 1, neither 2⁰ nor 2^-1 are powers of two. Under definition 2, 2⁰ is a power of two but 2^-1 is not. Under definition 3, both 2⁰ and 2^-1 are powers of two. In fact, under definition 3, two raised to any integer power is a power of two.

The different definitions crop up in different applications, depending on which set of values is required. However, if you want to discuss multiple applications in one context — like on this site — it makes sense to stick with one definition. Definition 3, the most inclusive definition, fits that role. We will adopt it as our standard definition.

The Powers of Two and Its Subsets

From the all-inclusive set we call the powers of two we can derive four aptly named subsets:

• The positive powers of two = {2ⁿ | n is an integer > 0}.
• The negative powers of two = {2ⁿ | n is an integer < 0}.
• The nonnegative powers of two = {2ⁿ | n is an integer ≥ 0}.
• The nonpositive powers of two = {2ⁿ | n is an integer ≤ 0}.

The name of each set corresponds to the range of exponents to which two is raised, describing each set precisely. This parallels how the integers themselves are named: the positive integers, the negative integers, the nonnegative integers, and the nonpositive integers.

In contexts where you would otherwise want to use definition 1, simply use “the positive powers of two” instead. Similarly, instead of definition 2, use “the nonnegative powers of two.”

Application to Binary Numbers

The main use for this broad definition of the powers of two is in the context of binary numbers. Compare the following statements — all equivalent — as they might be worded under each definition:

• Under definition 1: “The integer part of a binary number represents the number one or a sum of powers of two; the fractional part represents a sum of negative powers of two.”
• Under definition 2: “The integer part of a binary number represents a sum of powers of two; the fractional part represents a sum of negative powers of two.”
• Under definition 3: “A binary number represents a sum of powers of two.”

One job of a good definition is to make expressing ideas simpler; definition 3 certainly does that in this case.

Compared To The Powers of Ten

In contrast to the conflicting definitions of the powers of two, the powers of ten are widely recognized as {10ⁿ | n is an integer}. You will see this in the context of the decimal numbering system and scientific notation, for example. This is the equivalent of our broad definition of the powers of two, giving us consistency in this regard.

Summary

I made the case for defining a power of two as the number two raised to any integer power. This is the broadest definition that remains useful. It allows us to discuss all the applications in which we’re interested, using consistent terminology. This is the definition used on this site, and we would argue for its acceptance beyond that.

For more details on the definition, see “The Powers of Two.”