IntelliJ IDEA has a code inspection for Kotlin that will warn you if a decimal floating-point literal exceeds the precision of its type (Float or Double). It will suggest an equivalent literal (one that maps to the same binary floating-point number) that has fewer digits, or has the same number of digits but is closer to the floating-point number.
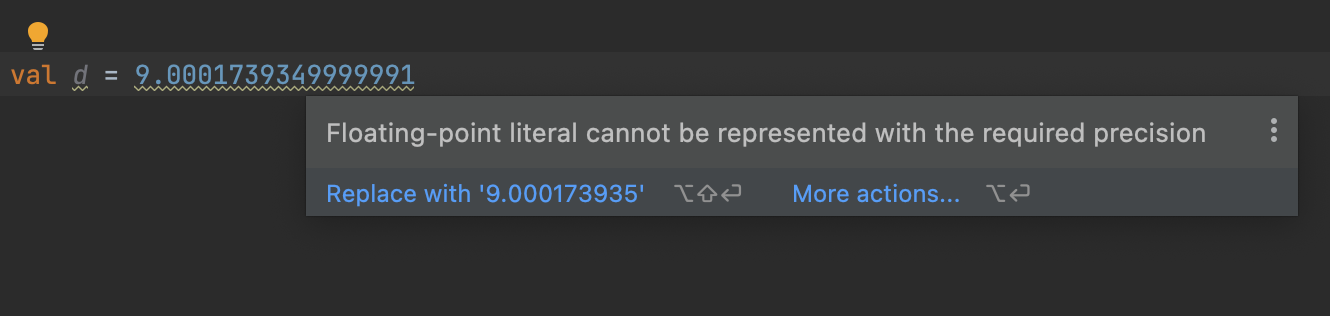
For Doubles for example, every literal over 17-digits should be flagged, since it never takes more than 17 digits to specify any double-precision binary floating-point value. Literals with 16 or 17 digits should be flagged if there is a replacement that is shorter or closer. And no literal with 15 digits or fewer should ever be flagged, since doubles have of 15-digits of precision.
But IntelliJ doesn’t always adhere to that, like when it suggests an 18-digit replacement for a 13-digit literal!

Enabling the Inspection
You can enable the inspection in IntelliJ IDEA by going to Preferences -> Editor -> Inspections -> Kotlin -> Other Problems and checking Floating-point literal exceeds the available precision. (The inspection was enabled by default for me.)
The Problem
Kotlin uses Java’s floating-point to decimal conversion routine, the dtoa() method of Java’s FloatingDecimal class. It has a 20-year old bug against it that is the source of the issue. I learned about this bug over six years ago, when writing “Java Doesn’t Print The Shortest Strings That Round-Trip”. When I recently encountered the Kotlin inspection I went back to that bug report and tried out some of its examples; here are eight literals that the inspection flagged, along with their suggested replacements:
| Ex. # | Literal | Digits | Replacement | Digits |
|---|---|---|---|---|
| 1 | 4.8726570057E288 | 11 | 4.8726570056999995E288 | 17 |
| 2 | 7.68905065813E17 | 12 | 7.6890506581299994E17 | 17 |
| 3 | 1.790086667993E18 | 13 | 1.79008666799299994E18 | 18 |
| 4 | 2.273317134858E18 | 13 | 2.27331713485799987E18 | 18 |
| 5 | 2.82879384806159E17 | 15 | 2.82879384806159008E17 | 18 |
| 6 | 1.45800632428665E17 | 15 | 1.45800632428664992E17 | 18 |
| 7 | 1.9400994884341945E25 | 17 | 1.9400994884341944E25 | 17 |
| 8 | 5.684341886080801486968994140625E-14 | 31 | 5.6843418860808015E-14 | 17 |
Examples 1-6 should not have been flagged, since they have 15 digits or fewer. Moreover, the replacements all have more digits.
Example 7 should not have been flagged either, because the replacement is another 17-digit number which is further than the original from the floating-point number. Written as integers, the original is 19400994884341945000000000, and the replacement is 19400994884341944000000000. Both convert to floating-point as 19400994884341944949932032 (the floating-point value written exactly in decimal). The original is closer to the floating-point value, with an absolute difference of 50,067,968 vs. 949,932,032.
In Example 8, the replacement is shorter than the original, but a one digit shorter replacement, 5.684341886080802E-14, would work as well, even though it’s further than the replacement from the floating-point number. This happens because the literal is a power of two (2-44). The gap size above a power of two is double the gap size below it, which in this case leads to a shorter replacement candidate that is not nearer.
Change in Format
Replacements could change format with respect to the original. For example, 123456789012345678E-16 becomes 12.345678901234567 (the “E” notation is removed), and 1234.56789012345678E-16 becomes 1.234567890123457E-13 (the number is normalized). This is not an error; it’s just a byproduct of FloatingDecimal’s dtoa() method’s rules for formatting, which are what they are.
How the Inspection Works
It was easy enough to determine how the inspection was implemented; the source code is on github. The code is simple, but I simplified it further for the purposes of this article, keeping only the logic for Doubles.
fun intellijFloatingPointLiteralPrecisionInspection(
literal: String
): String {
var replacement = literal.toDouble().toString()
val literalBD = BigDecimal(literal)
val replacementBD = BigDecimal(replacement)
if (literalBD == replacementBD)
replacement = ""
return replacement
}
The inspection relies entirely on the conversions done under the covers by the Java code, the decimal to floating-point conversion done by toDouble(), and the floating-point to decimal conversion done by toString(). The assumption is that the literal round-trips back from double-precision in its shortest or nearest form.
BigDecimal is used to factor out formatting differences between the literal and the replacement string that toString() returns. For example, if the literal is 5.198135943396802E6, the replacement is 5198135.943396802. Those are numerically equivalent, so there is no need to suggest a replacement.
Aside: The Literals Are Not Just Rounded
The implementation of the inspection demonstrates the principle I described in my article “17 Digits Gets You There, Once You’ve Found Your Way”. Literals greater than 17 digits can’t simply be rounded or truncated to 17 digits directly. Depending on how close the literal is to halfway between two binary floating point numbers, all of its digits may be needed to decide the correct Double to round to. The conversion done with toDouble() takes this into account. Once the floating point number is identified, its shortened “stand in” is generated by the return trip conversion, the toString() call.
Subnormal Numbers
Subnormal numbers change the rules in that they aren’t subject to the 15/16/17 digit boundaries described above; they have lower, variable effective precision. For example, 8.3616842E-322 has a suggested replacement of 8.35E-322, which is expected because the floating-point number has only 8 bits of precision.
(I did not look for anomalous replacements for subnormal numbers.)
The Solution
These examples would be addressed by a fix for the FloatingDecimal bug: return the shortest replacement or, if there isn’t a shorter one, return an equal-length replacement that is nearer to the floating-point value. (Coincidentally, this bug has been marked “resolved” as of June 2022, which I noticed as I was writing this article. I will look into it when it is released and incorporated into IntelliJ.)
Short of that proper fix, a workaround in the inspection itself could be to filter out most of the bad replacements. It could filter any replacement returned by toString() that has more digits than the original, and it could use BigDecimal to check whether an equal-length replacement is closer. Adding an else to the code above should take care of those two cases, addressing literals like Examples 1-7:
fun intellijFloatingPointLiteralPrecisionInspectionWorkAround(
literal: String
): String {
var replacement = literal.toDouble().toString()
val literalBD = BigDecimal(literal)
val replacementBD = BigDecimal(replacement)
if (literalBD == replacementBD)
replacement = ""
else {
// Filter out false positives
when {
literalBD.precision() < replacementBD.precision() -> replacement = ""
literalBD.precision() == replacementBD.precision() -> {
val doubleBD = BigDecimal(literal.toDouble())
val literalDeltaBD = (literalBD - doubleBD).abs()
val replacementDeltaBD = (replacementBD - doubleBD).abs()
if (literalDeltaBD <= replacementDeltaBD)
replacement = ""
}
}
}
return replacement
}
Coding a workaround for “shortest not nearest” cases like Example 8 would be harder. And it may not be worth the effort, since there are only 54 powers of two for which this comes into play.
Issue KTIJ-22245 Submitted
I submitted issue KTIJ-22245 against the IntelliJ IDEA Kotlin plugin.
Criticism of This Feature
If this inspection worked perfectly, I still don’t think I would find it useful. I encountered it while coding floating point literals to approximate logarithms. The originals can be more visually faithful to the actual decimal value. For example, log2(15) = 3.9068905956085185293…, which I coded (rounded to 17 digits) as 3.9068905956085185, had a suggested replacement of 3.9068905956085187. While both map to the same double-precision binary floating-point value (0x1.f414fdb498226p1), the original literal is closer in decimal, and is a correct decimal rounding of the logarithm; the replacement is not.
Also, Doubles don’t have 17 digits of precision (nor do they have 16 digits across the whole range of floating-point numbers). When the suggested replacement has 17 digits, it’s not really solving the “cannot be represented with the required precision” problem; it’s only giving what I have dubbed coincidental precision. This makes the name of the inspection itself questionable.
Perhaps a more generic name would be better: “Another literal can represent the same floating-point number”. That name would also have these benefits:
- It would make clear that the suggestion is optional, because you will get the same floating-point value either way.
- It might make it clearer why the replacement is not necessarily a decimal rounding of the literal.
- It would cover decimal literals that are exact in binary, for which the binary precision is never exceeded. For example, for 1.66667938232421875, which is exactly 1.10101010101010111 in binary (uses only 18 of the 53 bits of double-precision), the inspection suggests 1.6666793823242188, which is not terminating in binary, and ironically requires more (infinite) precision to represent exactly.
There probably is no perfect name, because to describe it exactly would take too many words: “A shorter or closer decimal literal can represent the same binary floating-point number”.
Other Floating-Point Literal Inspections


These are not accompanied by suggested replacements, but it would seem reasonable to suggest 0 for the “conforms to 0” case and either Double.MAX_VALUE or Double.POSITIVE_INFINITY (for positive numbers for example) for the “conforms to infinity” case.
Also, I would suggest a new inspection for subnormal numbers, warning of their lower precision (there would be no replacement to make).
