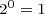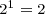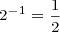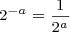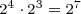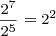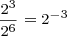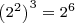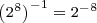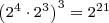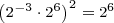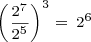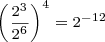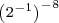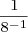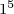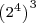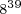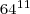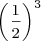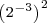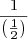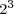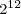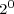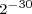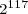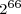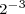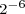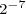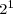Composing Powers of Two Using The Laws of Exponents

Powers of two can be combined, under the laws of exponents, to create other powers of two. Under these rules, you can multiply powers of two, divide powers of two, or raise a power of two to a power and still get another power of two. You can combine these rules to create complicated expressions, expressions that result in a single power of two. For example,

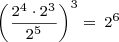$\mbox{\footnotesize{\displaystyle {{\left(\frac{2^4 \cdot 2^3}{2^5}\right)}^3 = \: 2^6}}}$ .

The laws of exponents apply generally to any base; two is no different. But since we’re interested in powers of two, we’ll couch them in terms of powers of two. Once we explain the laws in this way, you’ll understand the math behind the example above.

Basic Powers of Two Rules

The following are the basic rules of exponents for powers of two, rules you should be familiar with if you know what the powers of two are:

$\mbox{\footnotesize{\displaystyle {2^0 = 1}}}$
$\mbox{\footnotesize{\displaystyle {2^1 = 2}}}$
$\mbox{\footnotesize{\displaystyle {2^{-1} = \frac {1}{2}}}}$
$\mbox{\footnotesize{\displaystyle {2^{-a} = \frac {1}{2^a}}}}$
$\mbox{\footnotesize{\displaystyle {{\left(\frac {1}{2}\right)}^a = \frac {1}{2^a}}}}$

Rules For Combining Powers of Two

The following are the rules for combining powers of two under multiplication, division, and exponentiation:

Product of Powers of Two Rule: 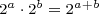$\mbox{\footnotesize{\displaystyle {{2^a} \cdot {2^b} = 2^{a+b}}}}$

This rule says a power of two multiplied by a power of two is a power of two. In particular, the resulting power of two has an exponent equal to the sum of the exponents of the multiplied powers of two.

Examples:

$\mbox{\footnotesize{\displaystyle {{2^4} \cdot {2^3} = 2^{7}}}}$
$\mbox{\footnotesize{\displaystyle {{2^{-3}} \cdot {2^6} = 2^{3}}}}$

Quotient of Powers of Two Rule: 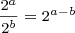$\mbox{\footnotesize{\displaystyle {\frac{2^a}{2^b} = 2^{a-b}}}}$

This rule says a power of two divided by a power of two is a power of two. In particular, the resulting power of two has an exponent equal to the dividend’s exponent minus the divisor’s exponent.

Examples:

$\mbox{\footnotesize{\displaystyle {\frac{2^7}{2^{5}} = 2^{2}}}}$
$\mbox{\footnotesize{\displaystyle {\frac{2^3}{2^{6}} = 2^{-3}}}}$

Power of a Power of Two Rule: 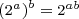$\mbox{\footnotesize{\displaystyle {\left({2^a}\right)}^{b} = 2^{ab}}}}$

This rule says a power of two raised to a power is a power of two. In particular, the resulting power of two has an exponent equal to the product of the two given exponents.

Examples:

$\mbox{\footnotesize{\displaystyle {\left({2^2}\right)}^3 = 2^{6}}}}$
$\mbox{\footnotesize{\displaystyle {\left({2^8}\right)}^{-1} = 2^{-8}}}}$

Composite Rules For Combining Powers of Two

In the general laws of exponents there are two additional rules: the power of a product rule and the power of a quotient rule. For powers of two, these rules become unnecessary, as they can be derived from the rules above. Nonetheless, they are still valid, and can provide a shortcut in calculations if you’re so inclined.

Power of a Product of Powers of Two Rule: 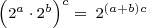$\mbox{\footnotesize{\displaystyle {\left({2^a \cdot 2^b}\right)}^{c} = \: 2^{\left(a+b\right)c}}}}$

This rule is just the combination of the product of powers of two rule and the power of a power of two rule.

Examples:

$\mbox{\footnotesize{\displaystyle {{\left(2^4 \cdot 2^3\right)}^3 = 2^{21}}}}$
$\mbox{\footnotesize{\displaystyle {{\left({2^{-3}} \cdot {2^6}\right)}^2 = 2^{6}}}}$

Power of a Quotient of Powers of Two Rule: 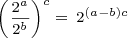$\mbox{\footnotesize{\displaystyle {\left({\frac{2^a}{2^b}}\right)^c = \: 2^{\left(a-b\right)c}}}}$

This rule is just the combination of the quotient of powers of two rule and the power of a power of two rule.

Examples:

$\mbox{\footnotesize{\displaystyle {{\left(\frac{2^7}{2^5}\right)}^3 = \: 2^6}}}$
$\mbox{\footnotesize{\displaystyle {{\left(\frac{2^3}{2^{6}}\right)}^4 = 2^{-12}}}}$

Powers of Two as Arbitrary Expressions

You can use the above rules to reduce complicated expressions to the form 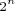$\mbox{\scriptsize{\displaystyle {2^n}}}$ . Let’s return to the example at the beginning of this article:

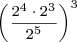
$\mbox{\footnotesize{\displaystyle {{\left(\frac{2^4 \cdot 2^3}{2^5}\right)}^3}}}$

There are several ways to reduce this. Here is a way without using any composite (shortcut) rules:

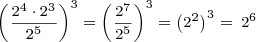
$\mbox{\footnotesize{\displaystyle {{\left(\frac{2^4 \cdot 2^3}{2^5}\right)}^3 = {\left(\frac{2^7}{2^5}\right)}^3 = \left({2^2}\right)^3 = \: 2^6}}}$

Here’s a way using a composite rule:

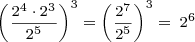
$\mbox{\footnotesize{\displaystyle {{\left(\frac{2^4 \cdot 2^3}{2^5}\right)}^3 = {\left(\frac{2^7}{2^5}\right)}^3 = \: 2^6}}}$

Here’s a longer way, which would have been longer without the use of a composite rule:

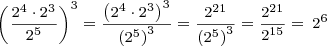
$\mbox{\footnotesize{\displaystyle {{\left(\frac{2^4 \cdot 2^3}{2^5}\right)}^3 = \frac{{\left(2^4 \cdot 2^3\right)}^3}{{\left(2^5\right)}^3} = \frac{2^{21}}{{\left(2^5\right)}^3} = \frac{2^{21}}{2^{15}} = \: 2^6}}}$

Transforming Numeric Powers of Two

If there are powers of two in an expression that appear numerically — for example, 64 instead of 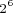$\mbox{\scriptsize{\displaystyle {2^6}}}$ — transform them to the form 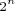$\mbox{\scriptsize{\displaystyle {2^n}}}$ . Then, apply the rules above. Here is an example:

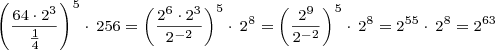$\mbox{\footnotesize{\displaystyle{{\left(\frac{64 \cdot 2^3}{\frac{1}{4}}\right)}^5}\cdot \: 256 = {\left(\frac{{2^6}\cdot{2^3}}{2^{-2}\right)}}^5}\cdot \: 2^8 = {\left(\frac{2^9}{2^{-2}\right)}}^5}\cdot \: 2^8 = 2^{55}\cdot \: 2^8 = 2^{63}}}}$ .

A Visual Example

You can see the laws of exponents in action in the following diagram:

A 4" x 4" x 4" cube. — A 4 in x 4 in x 4 in cube.

Here are three equivalent ways to compute the volume of the cube:

Length x width x height: 4 x 4 x 4 = 64 cubic inches
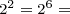Length x width x height: $\mbox{\footnotesize{\displaystyle {2^2}}}$ x $\mbox{\footnotesize{\displaystyle {2^2}}}$ x $\mbox{\footnotesize{\displaystyle {2^2 = 2^6 = }}}$ 64 cubic inches
Length cubed: 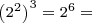$\mbox{\footnotesize{\displaystyle {{\left(2^2}\right)^3 = 2^6 = }}}$ 64 cubic inches

Here are three equivalent ways to compute the area of each side of the cube:

Length x width: 4 x 4 = 16 square inches
Length x width: 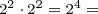$\mbox{\footnotesize{\displaystyle {2^2 \cdot 2^2 = 2^4 = }}}$ 16 square inches
Volume / height: 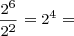$\mbox{\footnotesize{\displaystyle {\frac{2^6}{2^2} = 2^4 = }}}$ 16 square inches