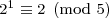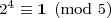Cycle Length of Powers of Two Mod Powers of Ten

In my article “Patterns in the Last Digits of the Positive Powers of Two” I noted that the positive powers of two modulo 10^m cycle with period 4·5^m-1, starting at 2^m. For example, the powers of two mod 10 cycle with period four: 2, 4, 8, 6, 2, 4, 8, 6, … . In this article, I’ll present my proof, which has two parts:

Part 1 shows that the powers of two mod 5^m cycle with period 4·5^m-1, starting at 2⁰.
Part 2 shows that the powers of two mod 10^m cycle with the same period as the powers of two mod 5^m, starting at 2^m.

To understand the proof, you’ll need to know some elementary number theory.

Part 1: Period mod 5^m is 4·5^m-1

The main goal of part 1 is to show that two is a primitive root mod powers of five, meaning that the order of 2 mod 5^m is the value of Euler’s phi function for 5^m. I break this into three steps, showing that

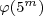$\mbox{\footnotesize{\displaystyle{\varphi (5^m)}}}$ = 4·5^m-1, where 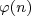$\mbox{\footnotesize{\displaystyle{\varphi (n)}}}$ is Euler’s phi function (also known as Euler’s totient function).
2 is a primitive root mod 5.
2 is a primitive root mod 5^m.

In addition, I show that the powers of two mod 5^m cycle starting at 2⁰; this is important because it will show that the cycle mod 10^m always starts after the cycle mod 5^m.

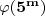$\mbox{\footnotesize{\displaystyle{\bf{\varphi (5^m)}}}}$ = 4·5^m-1

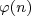$\mbox{\footnotesize{\displaystyle{\varphi (n)}}}$ is the number of positive integers less than or equal to n that are relatively prime to n. For a power of a prime number p, we can use this formula to compute it: 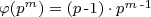$\mbox{\footnotesize{\displaystyle{\varphi (p^m) = (p \,$-$ 1) \cdot p^{m\,\textnormal{-}1}}}}$ . For p=5, this gives 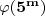$\mbox{\footnotesize{\displaystyle{\bf{\varphi (5^m)}}}}$ = 4·5^m-1.

2 is a Primitive Root Mod 5

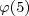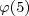To prove this, we just have to show that the order (also known as multiplicative order) of 2 mod 5 is equal to $\mbox{\footnotesize{\displaystyle{\varphi (5)}}}$ .

$\mbox{\footnotesize{\displaystyle{\varphi (5)}}}$ = 4, by the formula above. The order of 2 mod 5 — the smallest exponent a such that $\mbox{\footnotesize{\displaystyle{2^a \equiv 1 \pmod{5}}}}$ — is four, as shown by the following sequence of four calculations:

$\mbox{\footnotesize{\displaystyle{2^1 \equiv 2 \pmod{5}}}}$
$\mbox{\footnotesize{\displaystyle{2^2 \equiv 4 \pmod{5}}}}$
$\mbox{\footnotesize{\displaystyle{2^3 \equiv 3 \pmod{5}}}}$
$\mbox{\footnotesize{\displaystyle{2^4 \equiv \textbf{1} \pmod{5}}}}$

Thus, 2 is a primitive root mod 5.

2 is a Primitive Root Mod 5^m

To show that 2 is a primitive root mod all positive powers of 5, we can use this result from page 26 of “A Course in Computational Algebraic Number Theory” by Henri Cohen:

“…to find a primitive root modulo p^a for p an odd prime and a ≥ 2, proceed as follows: first compute g a primitive root modulo p …, then compute g₁ = g^p-1 mod p². If g₁ ≠ 1, g is a primitive root modulo p^a for every a…” .

In our case g = 2 and p = 5. We’ve already shown 2 to be a primitive root mod 5, so now all we need to show is that 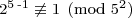$\mbox{\footnotesize{\displaystyle{2^{5\,\textnormal{-}1} \not \equiv 1 \pmod{5^2}}}}$ , which is trivial: $\mbox{\footnotesize{\displaystyle{2^4 \equiv 16 \pmod{25}}}}$ .

So, 2 is a primitive root mod 5^m, which means that the order of 2 mod 5^m is 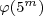$\mbox{\footnotesize{\displaystyle{\varphi (5^m)}}}$ . This proves that the powers of two mod 5^m cycle with period 4·5^m-1.

The Powers of Two Mod 5^m Cycle Starting at 2⁰

Let the period p = 4·5^m-1. 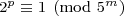$\mbox{\footnotesize{\displaystyle{2^p \equiv 1 \pmod{5^m}}}}$ , since 2 is a primitive root mod powers of 5 (Euler’s theorem applies). We also know, trivially, that 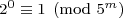$\mbox{\footnotesize{\displaystyle{2^0 \equiv 1 \pmod{5^m}}}}$ . The difference between the exponents p and 0 is p, showing a full cycle occurs starting at 2⁰.

Part 2: Period mod 10^m is 4·5^m-1

Part 2 shows, using the definition of modular arithmetic, the laws of exponents, and simple algebra, that the powers of two mod 10^m have the same period as the powers of two mod 5^m. It’s broken into two halves, showing that

The period mod 5^m is a cycle mod 10^m.
The cycle mod 10^m is the period mod 5^m.

The first half only shows that the period mod 5^m is a multiple of the period mod 10^m. The second half shows that the period mod 10^m is in fact the same as the period mod 5^m.

I’ll use the variable p for the period mod 5^m, as above, to simplify the notation in the proof that follows.

The period mod 5^m is a cycle mod 10^m

For i ≥ 0, what we’ve shown is that 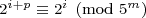$\mbox{\footnotesize{\displaystyle{2^{i+p} \equiv 2^i \pmod{5^m}}}}$ . That is, powers of two with exponents a period apart are congruent mod 5^m.

Congruence mod 5^m means that 2^i+p – 2ⁱ is a multiple of 5^m; that is, 2^i+p – 2ⁱ = n·5^m, for some nonnegative integer n.

Factoring out 2ⁱ we get 2ⁱ(2^p – 1) = n·5^m. When i≥m, n is a multiple of 2^m, so n = n’·2^m.

Substituting n’·2^m for n we get 2ⁱ(2^p – 1) = n’·2^m5^m = n’·10^m.

Reversing the process above, we can show congruence mod 10^m:

2ⁱ(2^p – 1) = 2^i+p – 2ⁱ = n’·10^m.

This shows that for i≥m, 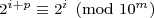$\mbox{\footnotesize{\displaystyle{2^{i+p} \equiv 2^i \pmod{10^m}}}}$ , so p is a cycle mod 10^m.

The cycle mod 10^m is the period mod 5^m

We’ve shown that p is a cycle mod 10^m, but not that p is the period mod 10^m. In other words, it’s possible the period mod 10^m is less than p — we have to show it isn’t.

For i ≥ m, we’ve shown that 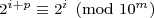$\mbox{\footnotesize{\displaystyle{2^{i+p} \equiv 2^i \pmod{10^m}}}}$ . Using the argument above, congruence mod 10^m means that:

2^i+p – 2ⁱ = n·10^m = n·2^m5^m = (n·2^m)5^m.

This shows that for i≥m, 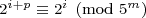$\mbox{\footnotesize{\displaystyle{2^{i+p} \equiv 2^i \pmod{5^m}}}}$ , so p is the period mod 5^m and mod 10^m.

Empirical Evidence that 2 is a Primitive Root mod 5^m

This section is not part of the proof, but it shows some PARI/GP calculations that support it.

These two commands show indirectly that 2 is a primitive root mod 5 through mod 5²⁰, by showing that the order equals Euler’s phi function:

? for(m=1,20,print(eulerphi(5^m)))
4
20
100
500
2500
12500
62500
312500
1562500
7812500
39062500
195312500
976562500
4882812500
24414062500
122070312500
610351562500
3051757812500
15258789062500
76293945312500

? for(m=1,20,print(znorder(Mod(2,5^m))))
4
20
100
500
2500
12500
62500
312500
1562500
7812500
39062500
195312500
976562500
4882812500
24414062500
122070312500
610351562500
3051757812500
15258789062500
76293945312500

This command shows directly that 2 is a primitive root mod powers of 5, using PARI/GP’s znprimroot() function (znprimroot only returns the lowest primitive root, which luckily for us is 2):

? for(m=1,20,print(znprimroot(5^m)))
Mod(2, 5)
Mod(2, 25)
Mod(2, 125)
Mod(2, 625)
Mod(2, 3125)
Mod(2, 15625)
Mod(2, 78125)
Mod(2, 390625)
Mod(2, 1953125)
Mod(2, 9765625)
Mod(2, 48828125)
Mod(2, 244140625)
Mod(2, 1220703125)
Mod(2, 6103515625)
Mod(2, 30517578125)
Mod(2, 152587890625)
Mod(2, 762939453125)
Mod(2, 3814697265625)
Mod(2, 19073486328125)
Mod(2, 95367431640625)

Summary

To prove the period formula for the positive powers of two mod powers of ten, I first proved it for mod powers of five. I showed that two is a primitive root mod powers of five, meaning that the period formula is Euler’s phi function for the powers of five. I then showed that the period mod powers of five and mod powers of ten must be the same, after a certain starting point.

References

These are the main influences behind my proof:

Challenging Mathematical Problems with Elementary Solutions, Volume 1. Page 198: “It can be proved that the last k digits of the number 2ⁿ are repeated in groups of 4·5^k-1, starting with the number 2^k.”
The USSR Olympiad Problem Book; Selected Problems and Theorems of Elementary Mathematics. Page 57, problem 243, and its answer, on page 354, discuss the case for powers of two mod 10¹⁰.
Question I asked at physicsforums.com. User hamster143’s proof that the period for powers of five and ten are equal.
Discussion at physicsforums.com. User shmoe’s comment: “a power of 2’s congruence class mod 10 is completely determined by its congruence class mod 5”.
Hakmem Item 57. Two comments by Schroeppel:
- “After the nth, they are all multiples of 2ⁿ.”
- “They get into a loop of length 4·5^m-1. (Because 2 is a primitive root of powers of 5.)”
Question I asked at mathoverflow.net.

Cycle Length of Powers of Two Mod Powers of Ten

Part 1: Period mod 5^m is 4·5^m-1