I see these from time to time, but I don’t always capture them; here’s one I saw recently while playing a podcast:
(According to Castbox, this is an error in the ad and is out of their control.)
Another NaN In the Wild
A Simple Binary To Decimal Converter App In Jetpack Compose
I’ve been learning Jetpack Compose and Kotlin (and Android for that matter) so I decided to create a simple binary conversion app to demonstrate how easy it is to create (at least basic) UI in Compose.
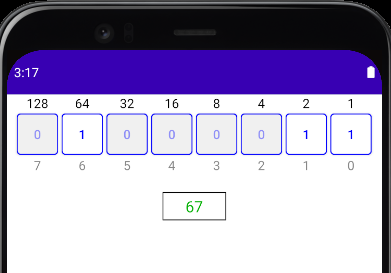
(This app has been updated; see Jetpack Compose Byte Converter App: 2022 Version.)
Continue reading “A Simple Binary To Decimal Converter App In Jetpack Compose”
Direct Generation of Double Rounding Error Conversions in Kotlin
For my recent search for short examples of double rounding errors in decimal to double to float conversions I wrote a Kotlin program to generate and test random decimal strings. While this was sufficient to find examples, I realized I could do a more direct search by generating only decimal strings with the underlying double rounding error bit patterns. I’ll show you the Java BigDecimal based Kotlin program I wrote for this purpose.
Continue reading “Direct Generation of Double Rounding Error Conversions in Kotlin”
Double Rounding Errors in Decimal to Double to Float Conversions
In my previous exploration of double rounding errors in decimal to float conversions I showed two decimal numbers that experienced a double rounding error when converted to float (single-precision) through an intermediate double (double-precision). I generated the examples indirectly by setting bit combinations that forced the error, using their corresponding exact decimal representations. As a result, the decimal numbers were long (55 digits each). Mark Dickinson derived a much shorter 17 digit example, but I hadn’t contemplated how to generate even shorter numbers — or whether they existed at all — until Per Vognsen wrote me recently to ask.
The easiest way for me to approach Per’s question was to search for examples, rather than try to find a way to construct them. As such, I wrote a simple Kotlin1 program to generate decimal strings and check them. I tested all float-range (including subnormal) decimal numbers of 9 digits or fewer, and tens of billions of random 10 to 17 digit float-range (normal only) numbers. I found example 7 to 17 digit numbers that, when converted to float through a double, suffer a double rounding error.
Continue reading “Double Rounding Errors in Decimal to Double to Float Conversions”
Google Doodle: Gottfried Wilhelm Leibniz
Google is celebrating Leibniz’s 372nd birthday today, recognizing him for his writings on binary numbers and binary arithmetic:
The drawing shows the binary code for the ASCII characters that spell “Google”:
Exploring Binary Now Supports HTTPS
I recently upgraded my ten year old site to support HTTPS. (I’d been waiting for my Web host to support Let’s Encrypt, the free certificate authority.)
Maximum Number of Decimal Digits In Binary Floating-Point Numbers
I’ve written about the formulas used to compute the number of decimal digits in a binary integer and the number of decimal digits in a binary fraction. In this article, I’ll use those formulas to determine the maximum number of digits required by the double-precision (double), single-precision (float), and quadruple-precision (quad) IEEE binary floating-point formats.
The maximum digit counts are useful if you want to print the full decimal value of a floating-point number (worst case format specifier and buffer size) or if you are writing or trying to understand a decimal to floating-point conversion routine (worst case number of input digits that must be converted).
Continue reading “Maximum Number of Decimal Digits In Binary Floating-Point Numbers”
Number of Decimal Digits In a Binary Fraction
The binary fraction 0.101 converts to the decimal fraction 0.625; the binary fraction 0.1010001 converts to the decimal fraction 0.6328125; the binary fraction 0.00111011011 converts to the decimal fraction 0.23193359375. In each of those examples, the binary fraction converts to a decimal fraction — that is, a terminating decimal representation — that has the same number of digits as the binary fraction has bits.
One digit per bit? We know that’s not true for binary integers. But it is true for binary fractions; every binary fraction of length n has a corresponding equivalent decimal fraction of length n.
This is the reason why you get all those “extra” digits when you print the full decimal value of an IEEE binary floating-point fraction, and why glibc strtod() and Visual C++ strtod() were once broken.
Continue reading “Number of Decimal Digits In a Binary Fraction”
Exploring Binary Is Now Mobile-Friendly
I recently upgraded my eight year old site to use a responsive design, making it mobile-friendly. I’ve kept the basic look of the site, although I retired the header image. The site is more readable, both on desktop and mobile devices.
17 Digits Gets You There, Once You’ve Found Your Way
Every double-precision floating-point number can be specified with 17 significant decimal digits or less. A simple way to generate this 17-digit number is to round the full-precision decimal value of the double to 17 digits. For example, the double-precision value 0x1.6d4c11d09ffa1p-3, which in decimal is 1.783677474777478899614635565740172751247882843017578125 x 10-1, can be recovered from the decimal floating-point literal 1.7836774747774789e-1. The extra digits are unnecessary, since they will only take you to the same double.
On the other hand, an arbitrary, arbitrarily long decimal literal rounded or truncated to 17 digits may not convert to the double-precision value it’s supposed to. This is a subtle point, one that has even tripped up implementers of widely used decimal to floating-point conversion routines (glibc strtod() and Visual C++ strtod(), for example).
Continue reading “17 Digits Gets You There, Once You’ve Found Your Way”
Decimal Precision of Binary Floating-Point Numbers
How many decimal digits of precision does a binary floating-point number have?
For example, does an IEEE single-precision binary floating-point number, or float as it’s known, have 6-8 digits? 7-8 digits? 6-9 digits? 6 digits? 7 digits? 7.22 digits? 6-112 digits? (I’ve seen all those answers on the Web.)
Continue reading “Decimal Precision of Binary Floating-Point Numbers”
Java Doesn’t Print The Shortest Strings That Round-Trip
I’ve always thought Java was one of the languages that prints the shortest decimal strings that round-trip back to floating-point. I was wrong.
Continue reading “Java Doesn’t Print The Shortest Strings That Round-Trip”
