Tag: Decimals

In my article “When Floats Don’t Behave Like Floats” I explained how calculations involving single-precision floating-point variables may be done, under the covers, in double or extended precision. This leads to anomalies in expected results, which I demonstrated with two C programs — compiled with Microsoft Visual C++ and run on a 32-bit Intel Core Duo processor.

In this article, I’ll do a similar analysis for double-precision floating-point variables, showing how similar anomalies arise when extended precision calculations are done. I modified my two example programs to use doubles instead of floats. Interestingly, the doubles version of program 2 does not exhibit the anomaly. I’ll explain.

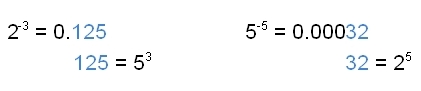
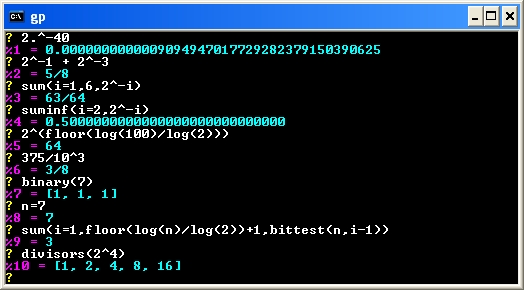
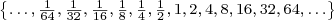Continue reading “When Doubles Don’t Behave Like Doubles”

These two programs — compiled with Microsoft Visual C++ and run on a 32-bit Intel Core Duo processor — demonstrate an anomaly that occurs when using single-precision floating point variables:

Program 1

#include "stdio.h"
int main (void)
{
 float f1 = 0.1f, f2 = 3.0f, f3;

 f3 = f1 * f2;
 if (f3 != f1 * f2)
   printf("Not equal\n");
}

Prints “Not equal”.

Program 2

#include "stdio.h"
int main (void)
{
 float f1 = 0.7f, f2 = 10.0f, f3;
 int i1, i2;

 f3 = f1 * f2;
 i1 = (int)f3;
 i2 = (int)(f1 * f2);
 if (i1 != i2)
   printf("Not equal\n");
}

Prints “Not equal”.

In each case, f3 and f1 * f2 differ. But why? I’ll explain what’s going on.

Continue reading “When Floats Don’t Behave Like Floats”