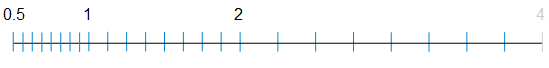Any double-precision floating-point number can be identified with at most 17 significant decimal digits. This means that if you convert a floating-point number to a decimal string, round it (to nearest) to 17 digits, and then convert that back to floating-point, you will recover the original floating-point number. In other words, the conversion will round-trip.
Sometimes (many) fewer than 17 digits will serve to round-trip; it is often desirable to find the shortest such string. Some programming languages generate shortest decimal strings, but many do not.1 If your language does not, you can attempt this yourself using brute force, by rounding a floating-point number to increasing length decimal strings and checking each time whether conversion of the string round-trips. For double-precision, you’d start by rounding to 15 digits, then if necessary to 16 digits, and then finally, if necessary, to 17 digits.
There is an interesting anomaly in this process though, one that I recently learned about from Mark Dickinson on stackoverflow.com: in rare cases, it’s possible to overlook the shortest decimal string that round-trips. Mark described the problem in the context of single-precision binary floating-point, but it applies to double-precision binary floating-point as well — or any precision binary floating-point for that matter. I will look at this anomaly in the context of double-precision floating-point, and give a detailed analysis of its cause.
Continue reading “The Shortest Decimal String That Round-Trips May Not Be The Nearest”