The Powers of Two

The following infinite set of numbers is known as the powers of two:

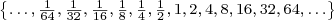$\mbox{\footnotesize{\left\{ {\ldots, \frac{1}{64}, \frac{1}{32}, \frac{1}{16}, \frac{1}{8}, \frac{1}{4}, \frac{1}{2}, 1, 2, 4, 8, 16, 32, 64, \ldots} \right\}}}$ .

Why are they called powers of two? What is the pattern you see? How is the set described mathematically? What are the set’s components? We will answer those questions in this article.

Let’s start by naming its three basic components, or subsets: the positive powers of two, the negative powers of two, and two to the zeroth power. These will serve as a guide through our explanation.

The Positive Powers of Two

Consider the set of numbers you get when you start with the number two and keep doubling: {2, 4, 8, 16, 32, 64, …}. This is the infinite set of positive integers known as the positive powers of two.

Why are numbers in this set called positive powers of two? First, what is a “positive power”? A positive power is another term for “positive exponent,” which is just shorthand for multiplication. Instead of 2·2·2·2·2, for example, you could write 2⁵. This reads “two raised to the fifth power” or “two to the fifth power” or simply “two to the fifth.” However you choose to say it, it means five twos multiplied together — 32. Since it is two we are raising to the power, we call 2⁵ a power of two; and more specifically in this case, a positive power of two.

In the order in which we’ve listed them, each positive power of two is two times the previous. You can show the factors of two explicitly by writing

{2, 2·2, 2·2·2, 2·2·2·2, 2·2·2·2·2, 2·2·2·2·2·2, …}.

Using exponents, you can rewrite it as {2¹, 2², 2³, 2⁴, 2⁵, 2⁶, …}. (Recall that 2¹ simply means 2 — no multiplication is involved.) Recognizing the pattern, we can write it more concisely as {2ⁿ | n is an integer > 0}, which reads “the set of all elements 2ⁿ such that n is a positive integer.”

The Negative Powers of Two

Consider the set of numbers you get when you start with the fraction 1/2 and keep halving: $\mbox{\footnotesize{\left\{ {\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \frac{1}{64}, \ldots} \right\}}}$ . Equivalently, consider the set of numbers you get when you start with the decimal fraction 0.5 and keep halving: {0.5, 0.25, 0.125, 0.0625, 0.03125, 0.015625, …}. In either form, this is the infinite set of positive fractions known as the negative powers of two.

Why are numbers in this set called negative powers of two? Well first of all, what is a negative power, or negative exponent? Surely it isn’t shorthand for multiplying a negative number of factors — that wouldn’t make sense. Then what, for example, does 2^-5 (two to the negative fifth or two to the minus fifth) mean? It means raise two to the fifth power and then invert it, giving 1/2⁵ = 1/32 = 0.03125. This inverse relationship is clear when you compare the sets {2, 4, 8, 16, 32, 64, …} and $\mbox{\footnotesize{\left\{ {\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \frac{1}{64}, \ldots} \right\}}}$ .

In the order in which we’ve listed them, each negative power of two is one-half the previous. You can show the factors of one-half explicitly by writing

$\mbox{\footnotesize{\left\{ {\frac{1}{2}, \, \frac{1}{2} {\cdot} \frac{1}{2}, \, \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2}, \, \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2}, \, \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2}, \, \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2} {\cdot} \frac{1}{2}, \, \ldots} \right\}}}$ .

If you combine the denominators you get

$\mbox{\footnotesize{\left\{ {\frac{1}{2}, \, \frac{1}{2 \cdot 2}, \, \frac{1}{2 \cdot 2 \cdot 2}, \, \frac{1}{2 \cdot 2 \cdot 2 \cdot 2}, \, \frac{1}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}, \, \frac{1}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}, \, \ldots} \right\}}}$ .

This can be expressed using positive exponents as

$\mbox{\footnotesize{\left\{ {\frac{1}{2^1}, \frac{1}{2^2}, \frac{1}{2^3}, \frac{1}{2^4}, \frac{1}{2^5}, \frac{1}{2^6}, \ldots} \right\}}}$ .

Recognizing these as negative exponents in disguise, you can rewrite it as {2^-1, 2^-2, 2^-3, 2^-4, 2^-5, 2^-6, …}. Written more concisely, this is {2ⁿ | n is an integer < 0}, which reads “the set of all elements 2ⁿ such that n is a negative integer.”

It’s worth emphasizing — the word “negative” qualifies the word “powers” and not the phrase “powers of two.” It is the power that is negative, not the power of two. We wouldn’t say, for example, that -8 is a negative power of two (although it is in a different sense — it’s a power of two that’s negative). Just remember — negative powers of two are positive numbers!

Two to The Zeroth Power

To this point we’ve discussed raising two to all integer powers except zero. So what is two to the zeroth power, or 2⁰? An exponent of zero does not have a neat interpretation like positive or negative exponents. It’s just defined to be one (so that exponent arithmetic works out). So like any number (except zero) raised to the zeroth power, 2⁰ = 1. So one is a power of two, and for our purposes we’ll refer to it as the one-element set {1} or {2⁰}.

If you combine the positive powers of two, the negative powers of two, and {2⁰} you get the set known collectively as the powers of two. This is the set of all elements 2ⁿ such that n is an integer, or {2ⁿ | n is an integer}. These are the values

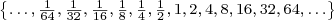$\mbox{\footnotesize{\left\{ {\ldots, \frac{1}{64}, \frac{1}{32}, \frac{1}{16}, \frac{1}{8}, \frac{1}{4}, \frac{1}{2}, 1, 2, 4, 8, 16, 32, 64, \ldots} \right\}}}$ ,

or equivalently, with fractions in decimal form,

{…, 0.015625, 0.03125, 0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 8, 16, 32, 64, …}.

You’ll notice that in this set we’ve written the negative powers of two in reverse. This is the standard way to display a set that is infinite in “both directions.” It corresponds to the orientation of the number line; the numbers get infinitely small as you go left and infinitely large as you go right. Also, it shows a simple relationship when written this way: for any two adjacent numbers, the one to the right is double the one to the left, or equivalently, the one to the left is half the one to the right.

Other partitions

It is sometimes convenient to partition the powers of two in other ways. For example, you can think of the set as being composed of just two subsets: the negative powers of two and the nonnegative powers of two. The nonnegative powers of two combine {2⁰} and the positive powers of two: {1, 2, 4, 8, 16, 32, 64, …} or {2ⁿ | n is an integer ≥ 0}. This breakdown is commonly used in the context of binary numbers, for example.

Similarly, you can think of the powers of two as being composed of the positive powers of two and the nonpositive powers of two. The nonpositive powers of two combine {2⁰} and the negative powers of two, and is written $\mbox{\footnotesize{\left\{1, {\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \frac{1}{64}, \ldots} \right\}}}$ or {2ⁿ | n is an integer ≤ 0}. This breakdown is not used commonly, however.

Summary

The following diagram summarizes what we’ve discussed:

The powers of two and its major subsets.

Here is the same, in symbols:

The powers of two = {2ⁿ | n is an integer}.
The positive powers of two = {2ⁿ | n is an integer > 0}.
The negative powers of two = {2ⁿ | n is an integer < 0}.
The nonnegative powers of two = {2ⁿ | n is an integer ≥ 0}.
The nonpositive powers of two = {2ⁿ | n is an integer ≤ 0}.

And now the same, in words:

A power of two is the number two raised to an integer power. A power of two is classified according to the sign of its exponent: positive, negative, nonnegative, or nonpositive. Powers of two are positive numbers. Nonnegative powers of two are integers, and negative powers of two are fractions. The negative powers of two are just the reciprocals of the positive powers of two, and are expressed as either proper fractions or decimals.

Endnotes

Competing Definitions

If this definition of the powers of two is broader than one you’ve seen it’s because there are other definitions in common use (see “A Standard Definition of The Powers of Two”).

Set vs. Sequence

Technically, we’re being loose about the distinction between a set and a sequence. A set describes its elements without specifying order, whereas a sequence describes a particular ordering of elements. {1, 2, 4} and {4, 1, 2} are the same set, but (1, 2, 4) and (4, 1, 2) are different sequences.

We’ve listed powers of two in a particular order and described properties of that ordering, which means we’ve implicitly defined a sequence as well — a geometric sequence in fact. Where this does not cause confusion, we will exploit this fact, as in phrases like “add the first six nonnegative powers of two.”

4 comments

Steve Pixton says:

November 19, 2008 at 9:01 pm

I recall in one of my calculus classes, when we were studying logs, natural logs, and the number e, the professor asked “why does e^0=1?”. I was the only one to raise my hand. I said “because any number raised to the zero = 1.” He was a bit taken aback, and said “true, but not what I was looking for.” Then he waited, until someone else said “because ln(1)= 0.” He said “right”. (You see, he had previously explained how if ln(x)=b, then e(ln(x))=e(b), then x=e(b). e to the ln of something “cancels”). I still like my answer better. So in binary, another answer to why is 2^0=1 is because log(base 2)(1)=0.
Rick Regan says:

November 20, 2008 at 3:28 pm

I haven’t enabled math in comments so we’ll have to do this without LaTeX….

Your answer IS better; his is circular. ln(1)=0 is the same as saying e^0=1, and e^0=1 is the same as saying ln(1)=0. But why is ln(1)=0, or equivalently, why is e^0=1? Because it’s defined that way. I said parenthetically in the article “so that exponent arithmetic works out.” Let me elaborate (I’ll put it in terms of base 2, but any base will do).

The laws of exponents say 2^a / 2^b = 2^(a-b). To make this rule work for a=b, you have to allow 2^0=1: 2^a/2^a = 1, so 2^(a-a) = 1, so 2^0 = 1.
sami morsi says:

September 22, 2011 at 7:18 am

dear Messers
Your presentation is very fascinating, easily absorbed especially for those people who do feel with mathematic phobia. Thank you so much, and much greetings from the first cairo, egypt.
John says:

April 1, 2015 at 7:26 pm

I would have answered because f(x) is both continuous and differentiable at f(0) = 1.

John Napier, who invented Napier’s bones, saw that if f(x) for all f(n) 0^n where f(x) is a power function is continuous at f(0) If and only if f(0) = 1 AND f(n) is not the zero power function. Newton and Lebinitz would later see the use of it in calculus.

x^x is continuous and differentiable over the entire interval ( -inf, +inf ) except x = 0. ( what is it at x = 0 ? )

Comments are closed.