Visual C++ and GLIBC strtod() Ignore Rounding Mode

When a decimal number is converted to a binary floating-point number, the floating-point number, in general, is only an approximation to the decimal number. Large integers, and most decimal fractions, require more significant bits than can be represented in the floating-point format. This means the decimal number must be rounded, to one of the two floating-point numbers that surround it.

Common practice considers a decimal number correctly rounded when the nearest of the two floating-point numbers is chosen (and when both are equally near, when the one with significant bit number 53 equal to 0 is chosen). This makes sense intuitively, and also reflects the default IEEE 754 rounding mode — round-to-nearest. However, there are three other IEEE 754 rounding modes, which allow for directed rounding: round toward positive infinity, round toward negative infinity, and round toward zero. For a conversion to be considered truly correctly rounded, it must honor all four rounding modes — whichever is currently in effect.

I evaluated the Visual C++ and glibc strtod() functions under the three directed rounding modes, like I did for round-to-nearest mode in my articles “Incorrectly Rounded Conversions in Visual C++” and “Incorrectly Rounded Conversions in GCC and GLIBC”. What I discovered was this: they only convert correctly about half the time — pure chance! — because they ignore the rounding mode altogether.

(Update 10/5/13: glibc strtod() honors rounding mode as of version 2.17.)

Example: Correct Rounding in All Four Rounding Modes

The diagram below shows how correct conversion works in each of the four rounding modes; I used the decimal values 0.1 and -0.1 as examples:

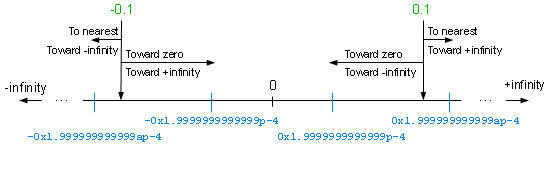
The conversions — shown in hexadecimal “%a” notation — were done by David Gay’s strtod() function and also verified by hand. In terms of absolute value, there are two different results; here they are in binary:

• 0x1.9999999999999p-4 =

  1.1001100110011001100110011001100110011001100110011001 x 2^-4

• 0x1.999999999999ap-4 =

  1.100110011001100110011001100110011001100110011001101 x 2^-4

Example: Incorrect Rounding in Visual C++ and glibc

Visual C++ and glibc strtod() do four of the eight conversions incorrectly:

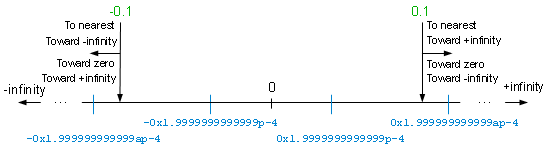
0.1, in round toward zero and round toward negative infinity modes, converts incorrectly to 0x1.999999999999ap-4. -0.1, in round toward zero and round toward positive infinity modes, converts incorrectly to -0x1.999999999999ap-4. That is, Visual C++ and glibc are converting 0.1 and -0.1 to a single absolute value in every case: 0x1.999999999999ap-4. That, not coincidentally, is the nearest floating-point number.

Visual C++ and glibc Always Round to Nearest

To see what percentage of conversions Visual C++ and glibc got right, I tested strtod() with random decimal values — both positive and negative — in each of the three directed rounding modes. I compared their results to those computed by David Gay’s strtod(). The percentage of incorrect conversions for both Visual C++ and glibc ranged between 49.00% and 49.06%, suggesting they were not reacting to the rounding mode at all. (Why it wasn’t almost exactly 50% I don’t know.) To confirm this, I generated random decimal values and converted each in all four modes; in every case, the four conversions were the same.

Conclusion: Visual C++ and glibc are using arbitrary-precision arithmetic in their calculations, and their algorithms are hard-coded to perform round-to-nearest rounding.

(Update: I was assuming David Gay’s strtod() got the conversions right in the directed rounding modes, but it turns out there was a bug — now fixed — that caused some conversions to come out incorrectly rounded. In any case, my conclusion is unaffected, since ultimately I didn’t need David Gay’s strtod() to reach it.)

Enabling Rounding Mode Detection in David Gay’s strtod()

David Gay’s strtod() function does not honor rounding mode by default; it must be enabled, by building dtoa.c with the flag “Honor_FLT_ROUNDS”. This forces the inclusion of file fenv.h, which defines the function fegetround(). fegetround() is called to get the current processor rounding mode, which strtod() uses to round its results correctly.

To make this work in Visual C++ — which doesn’t have the file fenv.h — I had to simulate fegetround(). I did this by calling _controlfp_s(&cur_cw,0,0) and translating the rounding mode masks (I am using the x87 FPU).

Conversion Algorithm Uses Floating-Point Arithmetic

David Gay’s strtod() function uses floating-point as well as arbitrary-precision calculations in its conversion, which you can see by reading the source code. You can also see this by building dtoa.c without “Honor_FLT_ROUNDS” and running it in the different rounding modes. Although the conversions won’t be correct (in general), they will differ, meaning they were computed with the help of the processor’s floating-point unit.

Discussion

Compile Time Vs. Run Time Conversions

I’ve been discussing strtod(), which does conversions at run time. But conversions can be done at compile time too — using floating-point literals. For the sake of argument, let’s say both strtod() and compile time conversions honor the current rounding mode (I don’t know if compile time conversions honor the rounding mode, but I expect they don’t). Assume also that both give the same result for the same rounding mode for the same decimal input. The compiled and strtod() conversions can still differ — if the rounding mode is different at run time than at compile time.

GLIBC Bug Report

The glibc bug report “Bugzilla Bug 3479: Incorrect rounding in strtod()” mentions, as an aside, strtod()’s failure to respond to the current rounding mode (see comment 6).

Update 10/5/13: Bug Now Fixed

glibc strtod() now honors rounding mode as of version 2.17. I reran my tests against glibc 2.18 and found no incorrect conversions.

Are There Any Applications That Depend on Directed Conversions?

Are there any Visual C++ or glibc based applications that depend on these “directed” conversions? I hope not — it doesn’t work.