The exact decimal equivalent of an arbitrary double-precision binary floating-point number is typically an unwieldy looking number, like this one:
0.1000000000000000055511151231257827021181583404541015625
In general, when you print a floating-point number, you don’t want to see all its digits; most of them are “garbage” in a sense anyhow. But how many digits do you need? You’d like a short string, yet you’d want it long enough so that it identifies the original floating-point number. A well-known result in computer science is that you need 17 significant decimal digits to identify an arbitrary double-precision floating-point number. If you were to round the exact decimal value of any floating-point number to 17 significant digits, you’d have a number that, when converted back to floating-point, gives you the original floating-point number; that is, a number that round-trips. For our example, that number is 0.10000000000000001.
But 17 digits is the worst case, which means that fewer digits — even as few as one — could work in many cases. The number required depends on the specific floating-point number. For our example, the short string 0.1 does the trick. This means that 0.1000000000000000055511151231257827021181583404541015625 and 0.10000000000000001 and 0.1 are the same, at least as far as their floating-point representations are concerned.
In this article, I will show you examples of decimal strings that can and can’t be shortened. (I will not discuss algorithms that are used to generate shortened strings; that will be the subject of future articles.)
Example 1: Only One Digit is Necessary
Let’s take a closer look at the 0.1 example; this diagram of the double-precision floating-point number line illustrates why it works:
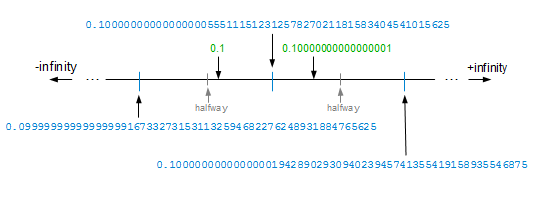
In blue are the exact decimal values of three floating point numbers: the middle one is my example number, the one to the left is the floating point number that precedes it, and the one to the right is the floating point number that follows it. In gray, I’ve marked the halfway points between the example number and its neighbors. Any value between these midpoints rounds to the example number. From this you can see, although 0.10000000000000001 is closer, 0.1 is still within rounding range; thus, 0.1 is preferable from the shortest string viewpoint.
Example 2: 17 Digits are Necessary
The floating point number 50388143.0682372152805328369140625 cannot be rounded to anything less than 17 digits and still round-trip. Rounded to 17 digits it’s 50388143.068237215, which converts back to our floating-point number. Rounded to 16 digits it’s 50388143.06823722, which is closer to the next floating-point number:
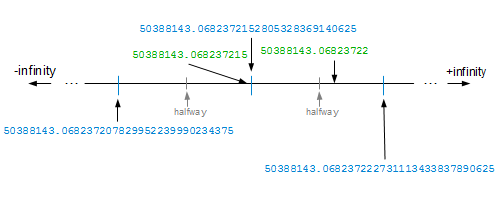
No shorter string exists, since rounding to lesser lengths will only introduce more error.
Example 3: Only 10 Digits are Necessary
The floating point number 54167628.179999999701976776123046875 can be rounded to 10 digits, but no less. Rounded to 10 digits it’s 54167628.18, which round-trips. Rounded to 9 digits, it’s 54167628.2, which won’t round-trip — it’s 2,684,355 binary ULPs away! (2,684,354 floating-point numbers stand between it and the one we want.)
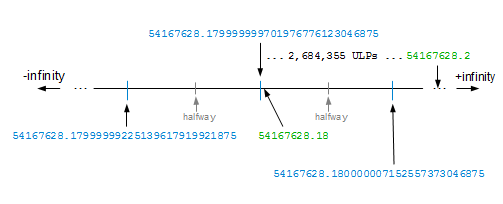
Example 4: Only 15 Digits are Necessary
The floating point number 9161196241250.05078125 can be rounded to as few as 15 digits (9161196241250.05) and still round-trip. Of course, it also round-trips rounded to 17 digits (9161196241250.0508) and 16 digits (9161196241250.051), which I’ve shown in the diagram.
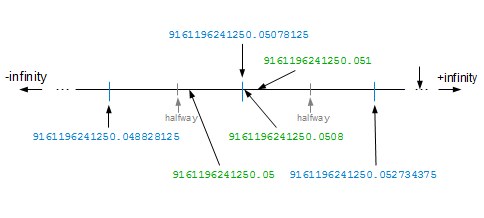
In this example, rounding to 17 digits gives a 17-digit string, rounding to 16 digits gives a 16-digit string, and rounding to 15 digits gives a 15-digit string. This is different from example 3 because 54167628.179999999701976776123046875 rounds to the 10-digit string 54167628.18 no matter whether it is rounded to 17, 16, 15, 14, 13, 12, 11, or 10 digits.

I find this interesting (along with your other posts). In .NET, I sometimes convert singles or doubles to decimals and want the shortest round trip decimal, as this is likely the “correct” decimal, being that people are basically storing decimals in the binary floats in the database. When converting from float to decimal, I don’t want the decimal to hold the closest number it can hold that most matches the Base 2 value. Rather, I want to assume the Base 2 number was the closest match to a Base 10 value. I want the decimal so that math looks correct. (User requirement.) Currently, I am calling the double.ToString(“R”) function, and then converting that to decimal. I’m trying to learn or search to see if there is a better/faster method, as it seems converting to a string would slow things down. You mentioned future posts may have algorithms for calculating the shortest round trip conversion. I will enjoy such posts, if you find time to write them. Thank you.
@Josh,
“I want to assume the Base 2 number was the closest match to a Base 10 value” is a good way to look at it.
Writing about rounding algorithms for the shortest strings is still on my todo list; I plan to write about these three papers:
It would be nice if double.ToString(“R”) implemented one of these algorithms, but I don’t think so based on its description. (BTW, you say you call it and then ‘convert that to decimal’ — what do you mean?)
It will be a while before I get to writing about this. In any case, I doubt you’ll want to write this code yourself.
Thank you for that information. I will definitely look it over. It has been a difficult topic to Google well…
Ok, I did find what seems to be a valid link to your first broken link: http://www.cs.indiana.edu/~dyb/pubs/FP-Printing-PLDI96.pdf
As for using ToString(“R”), basically i do this:
Dim myDecimal = CDec(myDoubleValue.ToString(“R”))
Which to my understanding is the shortest decimal that converts to the double, and seems to work. (Obviously, converting to a string and back to a number value doesn’t sound like the fastest way to do this…)
Also, I have a function like this for Single to Decimal.
And actually, the function from Double to Decimal detects if a Single was stored in the Double, and if so, converts to a Single before applying ToString(“R”)…
Of course, with that all said, I understand only a small fraction of this topic…
@Josh,
I understand now. When you said ‘decimal’ I thought you meant decimal string; now I see you mean numeric decimal.
> The floating point number 9161196241250.05078125 can be rounded to as few as 15 digits (9161196241250.05) and still round-trip. Of course, it also round-trips rounded to 17 digits (9161196241250.0508) and 16 digits (9161196241250.051)
It is really surprise. I write in Perl the Procedure FP3 the “How to Print Floating-Point Numbers Accurately” by Guy L. Steele Jr. It program prints 9161196241250.0508. It is the shortest 9161196241250.05.
@water qian,
Interesting. I have not implemented the Steele and White algorithm (yet). But David Gay’s dtoa() in modes 0 and 1 gives 9161196241250.05, as does Burger and Dybvig’s code (see their code and paper).
It would be interesting if you could write a Perl version of Burger and Dybvig’s code and compare that to your Steele and White implementation. Or at least maybe you could find more examples that (your implementation of) Steele and White get wrong and try to find out why.
I will look into the paper again and see where my program goes wrong. I suspect it might be my code because I saw the proof of the algorithm FP3 in Steele and White’s paper. It might be not easy to find it out and may take some time.
@Rick Regan,
I still have no time to carefully check what the issue is with the Perl code. However, the original Algorithm FP3 is only for pure fraction printout and I carelessly made an extension to print all floating. The issue must be the extension which is not proved. The number 9161196241250.05 is not pure fraction.
I have confirmed the issue is the scale factor I added. After I write it according to Algorithm Dragon2, it shows the shortest number correctly.
Water,
Thanks for keeping me posted!