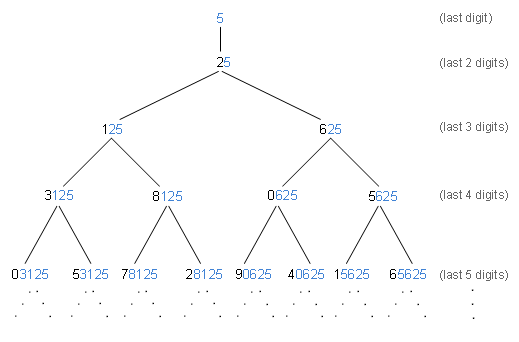
In my article “Patterns in the Last Digits of the Positive Powers of Five” I showed that the cycles of ending digits of the positive powers of five could be represented with a binary tree:
Binary Tree Showing Nested Ending Digit Patterns of the Positive Powers of Five
The tree layout shows that certain pairs of ending digits are related, and that these pairs differ by five in their starting digits. I will show why this is true.
In my article “Patterns in the Last Digits of the Positive Powers of Five” I noted that the positive powers of five modulo 10m cycle with period 2m-2, m ≥ 2, starting at 5m. In this article, I’ll present my proof, which has two parts:
The highlight of my proof is in part 1, where I derive a formula to show that the period, or order, of 5 mod 2m is 2m-2. While it is in general not possible to derive a formula for the order of a number, I’ll show it is possible for the powers of five mod 2m — due to a hidden, binary structure I’ve uncovered.
The positive powers of five — 5, 25, 125, 625, 3125, 15625, … — have a compact, repeating pattern in their ending m digits, in the powers of five from 5m on. For example: starting with 5, their last digit is always 5; starting with 25, their last two digits are always 25; starting with 125, their last three digits alternate between 125 and 625. These cycles come in lengths of powers of two.
Cycles in the Ending Digits of the Powers of Five
I will show you why these cycles exist, how they are expressed mathematically, and how to visualize them.
In my article “Patterns in the Last Digits of the Positive Powers of Two” I noted that the positive powers of two modulo 10m cycle with period 4·5m-1, starting at 2m. For example, the powers of two mod 10 cycle with period four: 2, 4, 8, 6, 2, 4, 8, 6, … . In this article, I’ll present my proof, which has two parts:
A common exercise in number theory is to find the last digits of a large power, like 22009, without using a computer. 22009 is a 605-digit number, so evaluating it by hand is out of the question. So how do you find its last digits — efficiently?
Modular arithmetic, and in particular, modular exponentiation, comes to the rescue. It provides an efficient way to find the last m digits of a power, by hand, with perhaps only a little help from a pocket calculator. All you need to do is compute the power incrementally, modulo 10m.
In this article, I will discuss three methods — all based on modular exponentiation and the laws of exponents — for finding the ending digits of a positive power of two. The techniques I use are easily adapted to powers of any number.
The positive powers of two — 2, 4, 8, 16, 32, 64, 128, 256, … — follow an obvious repeating pattern in their ending digit: 2, 4, 8, 6, 2, 4, 8, 6, … . This cycle of four digits continues forever. There are also cycles beyond the last digit — in the last m digits in fact — in the powers of two from 2m on. For example, the last two digits repeat in a cycle of length 20 starting with 04, and the last three digits repeat in a cycle of length 100 starting with 008.
In this article, I will show you why these cycles exist, how long they are, how they are expressed mathematically, and how to visualize them.
In my article “Nines in Binary”, I proved the following: positive integers of the form 10n-1, that is, integers made up of n digits of 9s, have binary representations with exactly n digits of trailing 1s. Pat Ballew made a clever observation, adapting my result to prove an equivalent statement for base 5 (quinary): positive integers of the form 10n-1 have quinary representations that have exactly n digits of trailing 4s. For example, 9999 in decimal is 304444 in quinary.
In “Nines in Binary”, I derived an expression for 10n – 1 that shows its structure as a binary number:
10n – 1 = (5n – 1) 2n + (2n – 1)
Pat derived a similar expression for 10n – 1 that shows its structure as a quinary number:
10n – 1 = (2n – 1) 5n + (5n – 1)
In essence, he swapped the 2s and 5s, making it the “dual” of my formula, if you will.
I’ll show the details of the derivation and prove why the formula works.
