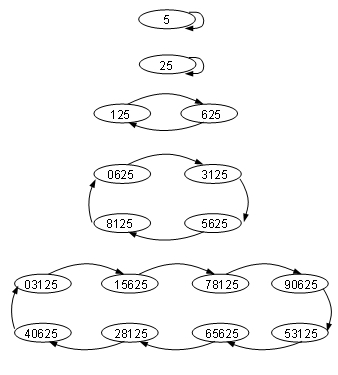
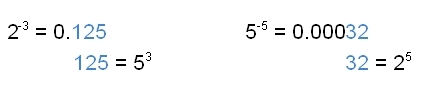Articles from 2009 - Exploring Binary

Cycle Length of Powers of Five Mod Powers of Ten

By Rick Regan December 22nd, 2009

In my article “Patterns in the Last Digits of the Positive Powers of Five” I noted that the positive powers of five modulo 10^m cycle with period 2^m-2, m ≥ 2, starting at 5^m. In this article, I’ll present my proof, which has two parts:

Part 1 shows that the powers of five mod 2^m cycle with period 2^m-2, m ≥ 2, starting at 5⁰.
Part 2 shows that the powers of five mod 10^m cycle with the same period as the powers of five mod 2^m, starting at 5^m.

The highlight of my proof is in part 1, where I derive a formula to show that the period, or order, of 5 mod 2^m is 2^m-2. While it is in general not possible to derive a formula for the order of a number, I’ll show it is possible for the powers of five mod 2^m — due to a hidden, binary structure I’ve uncovered.

Continue reading “Cycle Length of Powers of Five Mod Powers of Ten”

Binary Dates in 2010 and 2011

By Rick Regan December 19th, 2009

People have been tweeting about the upcoming dates that look like binary numbers. 10/10/10 seems to be a favorite, both because of its symmetry and because 101010 = 42 in decimal (you know, the answer to the ultimate question of life, the universe, and everything). Here are the nine dates in 2010, interpreted as binary numbers, and with their decimal equivalents:

Continue reading “Binary Dates in 2010 and 2011”

Patterns in the Last Digits of the Positive Powers of Five

By Rick Regan December 11th, 2009

The positive powers of five — 5, 25, 125, 625, 3125, 15625, … — have a compact, repeating pattern in their ending m digits, in the powers of five from 5^m on. For example: starting with 5, their last digit is always 5; starting with 25, their last two digits are always 25; starting with 125, their last three digits alternate between 125 and 625. These cycles come in lengths of powers of two.

Cycles in the Ending Digits of the Powers of Five

I will show you why these cycles exist, how they are expressed mathematically, and how to visualize them.

Continue reading “Patterns in the Last Digits of the Positive Powers of Five”

Seeing Powers of Five in Powers of Two and Vice Versa

By Rick Regan November 16th, 2009

The decimal representations of oppositely signed powers of two and powers of five look alike, as seen in these examples: 2^-3 = 0.125 and 5³ = 125; 5^-5 = 0.00032 and 2⁵ = 32. The significant digits in each pair of powers is the same, even though one is a fraction and one is an integer. In other words, a negative power of one base looks like a positive power of the other.

Powers of Two and Powers of Five that Look Alike

This relationship is not coincidence; it’s a by-product of how fractions are represented as decimals. I’ll show you simple algebra that proves it, as well as algebra that proves similar properties — in products involving negative powers.

Continue reading “Seeing Powers of Five in Powers of Two and Vice Versa”

Cycle Length of Powers of Two Mod Powers of Ten

By Rick Regan November 6th, 2009

In my article “Patterns in the Last Digits of the Positive Powers of Two” I noted that the positive powers of two modulo 10^m cycle with period 4·5^m-1, starting at 2^m. For example, the powers of two mod 10 cycle with period four: 2, 4, 8, 6, 2, 4, 8, 6, … . In this article, I’ll present my proof, which has two parts:

Part 1 shows that the powers of two mod 5^m cycle with period 4·5^m-1, starting at 2⁰.
Part 2 shows that the powers of two mod 10^m cycle with the same period as the powers of two mod 5^m, starting at 2^m.

Continue reading “Cycle Length of Powers of Two Mod Powers of Ten”

Floating-Point Error in the NPR Media Player

By Rick Regan October 31st, 2009

The NPR Media Player apparently uses floating-point numbers to represent timestamps, based on this image (click it to enlarge):

NaNs in NPR Media Player (thumbnail) — NaNs in NPR Media Player (click image to enlarge).

Continue reading “Floating-Point Error in the NPR Media Player”

My Custom Binary Themed Calendar for 2010

By Rick Regan October 26th, 2009

I found twelve free stock images — all with binary themes — and made a custom calendar for 2010. Here’s May:

Continue reading “My Custom Binary Themed Calendar for 2010”

How to Find the Last Digits of a Positive Power of Two

By Rick Regan October 14th, 2009

A common exercise in number theory is to find the last digits of a large power, like 2²⁰⁰⁹, without using a computer. 2²⁰⁰⁹ is a 605-digit number, so evaluating it by hand is out of the question. So how do you find its last digits — efficiently?

Modular arithmetic, and in particular, modular exponentiation, comes to the rescue. It provides an efficient way to find the last m digits of a power, by hand, with perhaps only a little help from a pocket calculator. All you need to do is compute the power incrementally, modulo 10^m.

In this article, I will discuss three methods — all based on modular exponentiation and the laws of exponents — for finding the ending digits of a positive power of two. The techniques I use are easily adapted to powers of any number.

Continue reading “How to Find the Last Digits of a Positive Power of Two”

Patterns in the Last Digits of the Positive Powers of Two

By Rick Regan September 27th, 2009

The positive powers of two — 2, 4, 8, 16, 32, 64, 128, 256, … — follow an obvious repeating pattern in their ending digit: 2, 4, 8, 6, 2, 4, 8, 6, … . This cycle of four digits continues forever. There are also cycles beyond the last digit — in the last m digits in fact — in the powers of two from 2^m on. For example, the last two digits repeat in a cycle of length 20 starting with 04, and the last three digits repeat in a cycle of length 100 starting with 008.

In this article, I will show you why these cycles exist, how long they are, how they are expressed mathematically, and how to visualize them.

Continue reading “Patterns in the Last Digits of the Positive Powers of Two”

Nines in Quinary

By Rick Regan September 8th, 2009

In my article “Nines in Binary”, I proved the following: positive integers of the form 10ⁿ-1, that is, integers made up of n digits of 9s, have binary representations with exactly n digits of trailing 1s. Pat Ballew made a clever observation, adapting my result to prove an equivalent statement for base 5 (quinary): positive integers of the form 10ⁿ-1 have quinary representations that have exactly n digits of trailing 4s. For example, 9999 in decimal is 304444 in quinary.

In “Nines in Binary”, I derived an expression for 10ⁿ – 1 that shows its structure as a binary number:

10ⁿ – 1 = (5ⁿ – 1) 2ⁿ + (2ⁿ – 1)

Pat derived a similar expression for 10ⁿ – 1 that shows its structure as a quinary number:

10ⁿ – 1 = (2ⁿ – 1) 5ⁿ + (5ⁿ – 1)

In essence, he swapped the 2s and 5s, making it the “dual” of my formula, if you will.

I’ll show the details of the derivation and prove why the formula works.

Continue reading “Nines in Quinary”

Finding Numbers That Are Palindromic In Multiple Bases

By Rick Regan September 1st, 2009

A palindromic number, or number palindrome, is a number like 74347, which is the same written forward and backward.

A number can be palindromic in any base, not just decimal. For example, 101101 is a palindrome in binary. A number can also be palindromic in more than one base, like decimal 719848917, which is 101010111010000000010111010101 in binary and 5272002725 in octal.

An efficient way to find palindromes in a single base is to generate them, iterating through each integer and constructing palindromes from them. An efficient way to find numbers that are palindromic in multiple bases is to take a palindrome in one base and test if it’s a palindrome in one or more additional bases.

In this article, I’ll show you C code I wrote that finds multi-base numeric palindromes. I used this code to generate tables of numbers that are palindromic in decimal and binary, decimal and hexadecimal, and decimal and octal. I also used this code to solve Euler problem 36, which asks for the sum of all numbers, less than one million, that are palindromic in decimal and binary.

Continue reading “Finding Numbers That Are Palindromic In Multiple Bases”

Exploring Binary Numbers With PARI/GP Calculator

By Rick Regan August 15th, 2009

PARI/GP is an open source computer algebra system I use frequently in my study of binary numbers. It doesn’t manipulate binary numbers directly — input, and most output, is in decimal — so I use it mainly to do the next best thing: calculate with powers of two. Calculations with powers of two are, indirectly, calculations with binary numbers.

PARI/GP is a sophisticated tool, with several components — yet it’s easy to install and use. I use its command shell in particular, the PARI/GP calculator, or gp for short. I will show you how to use simple gp commands to explore binary numbers.

PARI/GP Calculator (Example Calculations) (My Setup on Windows) — PARI/GP Calculator (Sample of Calculations Used to Explore Binary Numbers)

Continue reading “Exploring Binary Numbers With PARI/GP Calculator”