Binary Numbers, Binary Code, and Binary Logic
Articles About the Powers of Two and Their Mathematical Properties
I showed how the positive powers of ten and two are interleaved, and said that the interleaving of the negative powers of ten and two is its mirror image. In this article, I will show you why, and prove that the same properties hold.
Continue reading “How the Negative Powers of Ten and Two Are Interleaved”
To truly understand decimal to binary and binary to decimal conversion, you should know how the powers of ten and the powers of two relate. In particular, you should know how they are interleaved. The interleaving explains why, for example, the number of bits required to represent an n-digit decimal integer varies. Consequently, it also explains why 9,007,199,254,740,991 (253 – 1) is representable in binary floating-point, and why 9,007,199,254,740,993 (253 + 1) is not.
In this article, I will discuss the interleaving of the positive powers of ten and two, and prove some properties of it. (The interleaving of the negative powers is the mirror image of the positive powers, centered around 100 = 20 = 1.)
Continue reading “How the Positive Powers of Ten and Two Are Interleaved”
In my article “Composing Powers of Two Using The Laws of Exponents” I showed how to combine powers of two using the standard laws of exponents. There are two other rules I use when combining powers of two; I call them the add duplicate power of two rule and the subtract half power of two rule. These are nonstandard rules, applying only to powers of two. Although these are special cases of the existing multiplication and division rules, I’ve found value in recognizing them in addition and subtraction form. I’ll state these rules and show examples of their usage.
Continue reading “Special Case Laws of Exponents for Powers of Two”
In the children’s book “One Grain of Rice: A Mathematical Folktale” a girl uses her knowledge of exponential growth to trick a greedy king into turning over his stockpile of rice. Hidden in the story are mathematical concepts related to doubling: powers of two, geometric sequences, geometric series, and exponents. I will analyze the story from this perspective, and then discuss my experience reading it to first and third grade students.
In my article “Patterns in the Last Digits of the Positive Powers of Five” I showed that the cycles of ending digits of the positive powers of five could be represented with a binary tree:
The tree layout shows that certain pairs of ending digits are related, and that these pairs differ by five in their starting digits. I will show why this is true.
Continue reading “Ending Digits of Powers of Five Form a Binary Tree”
In my article “Patterns in the Last Digits of the Positive Powers of Five” I noted that the positive powers of five modulo 10m cycle with period 2m-2, m ≥ 2, starting at 5m. In this article, I’ll present my proof, which has two parts:
The highlight of my proof is in part 1, where I derive a formula to show that the period, or order, of 5 mod 2m is 2m-2. While it is in general not possible to derive a formula for the order of a number, I’ll show it is possible for the powers of five mod 2m — due to a hidden, binary structure I’ve uncovered.
Continue reading “Cycle Length of Powers of Five Mod Powers of Ten”
The positive powers of five — 5, 25, 125, 625, 3125, 15625, … — have a compact, repeating pattern in their ending m digits, in the powers of five from 5m on. For example: starting with 5, their last digit is always 5; starting with 25, their last two digits are always 25; starting with 125, their last three digits alternate between 125 and 625. These cycles come in lengths of powers of two.
I will show you why these cycles exist, how they are expressed mathematically, and how to visualize them.
Continue reading “Patterns in the Last Digits of the Positive Powers of Five”
The decimal representations of oppositely signed powers of two and powers of five look alike, as seen in these examples: 2-3 = 0.125 and 53 = 125; 5-5 = 0.00032 and 25 = 32. The significant digits in each pair of powers is the same, even though one is a fraction and one is an integer. In other words, a negative power of one base looks like a positive power of the other.
This relationship is not coincidence; it’s a by-product of how fractions are represented as decimals. I’ll show you simple algebra that proves it, as well as algebra that proves similar properties — in products involving negative powers.
Continue reading “Seeing Powers of Five in Powers of Two and Vice Versa”
In my article “Patterns in the Last Digits of the Positive Powers of Two” I noted that the positive powers of two modulo 10m cycle with period 4·5m-1, starting at 2m. For example, the powers of two mod 10 cycle with period four: 2, 4, 8, 6, 2, 4, 8, 6, … . In this article, I’ll present my proof, which has two parts:
Continue reading “Cycle Length of Powers of Two Mod Powers of Ten”
A common exercise in number theory is to find the last digits of a large power, like 22009, without using a computer. 22009 is a 605-digit number, so evaluating it by hand is out of the question. So how do you find its last digits — efficiently?
Modular arithmetic, and in particular, modular exponentiation, comes to the rescue. It provides an efficient way to find the last m digits of a power, by hand, with perhaps only a little help from a pocket calculator. All you need to do is compute the power incrementally, modulo 10m.
In this article, I will discuss three methods — all based on modular exponentiation and the laws of exponents — for finding the ending digits of a positive power of two. The techniques I use are easily adapted to powers of any number.
Continue reading “How to Find the Last Digits of a Positive Power of Two”
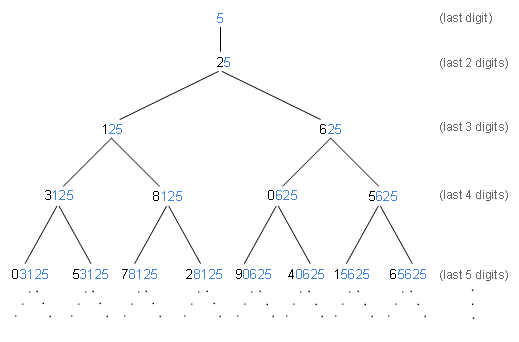
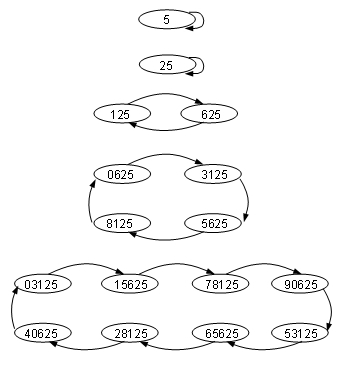
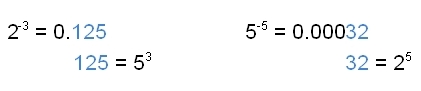The positive powers of two — 2, 4, 8, 16, 32, 64, 128, 256, … — follow an obvious repeating pattern in their ending digit: 2, 4, 8, 6, 2, 4, 8, 6, … . This cycle of four digits continues forever. There are also cycles beyond the last digit — in the last m digits in fact — in the powers of two from 2m on. For example, the last two digits repeat in a cycle of length 20 starting with 04, and the last three digits repeat in a cycle of length 100 starting with 008.
In this article, I will show you why these cycles exist, how long they are, how they are expressed mathematically, and how to visualize them.
Continue reading “Patterns in the Last Digits of the Positive Powers of Two”
PARI/GP is an open source computer algebra system I use frequently in my study of binary numbers. It doesn’t manipulate binary numbers directly — input, and most output, is in decimal — so I use it mainly to do the next best thing: calculate with powers of two. Calculations with powers of two are, indirectly, calculations with binary numbers.
PARI/GP is a sophisticated tool, with several components — yet it’s easy to install and use. I use its command shell in particular, the PARI/GP calculator, or gp for short. I will show you how to use simple gp commands to explore binary numbers.
Continue reading “Exploring Binary Numbers With PARI/GP Calculator”
