Binary Numbers, Binary Code, and Binary Logic
I wrote a simple byte to decimal converter app less than two months into starting to learn Jetpack Compose. Now that I have more experience with Compose — in developing a real app and by participating on the #compose channel on Slack (login required) — I wanted to update this demo app to reflect my current understanding of best practices.
Continue reading “Jetpack Compose Byte Converter App: 2022 Version”
IntelliJ IDEA has a code inspection for Kotlin that will warn you if a decimal floating-point literal exceeds the precision of its type (Float or Double). It will suggest an equivalent literal (one that maps to the same binary floating-point number) that has fewer digits, or has the same number of digits but is closer to the floating-point number.
For Doubles for example, every literal over 17-digits should be flagged, since it never takes more than 17 digits to specify any double-precision binary floating-point value. Literals with 16 or 17 digits should be flagged if there is a replacement that is shorter or closer. And no literal with 15 digits or fewer should ever be flagged, since doubles have of 15-digits of precision.
But IntelliJ doesn’t always adhere to that, like when it suggests an 18-digit replacement for a 13-digit literal!
Continue reading “Anomalies In IntelliJ Kotlin Floating-Point Literal Inspection”
I’ve been learning Jetpack Compose and Kotlin (and Android for that matter) so I decided to create a simple binary conversion app to demonstrate how easy it is to create (at least basic) UI in Compose.
(This app has been updated; see Jetpack Compose Byte Converter App: 2022 Version.)
Continue reading “A Simple Binary To Decimal Converter App In Jetpack Compose”
Google is celebrating Leibniz’s 372nd birthday today, recognizing him for his writings on binary numbers and binary arithmetic:
The drawing shows the binary code for the ASCII characters that spell “Google”:
I’ve written about the formulas used to compute the number of decimal digits in a binary integer and the number of decimal digits in a binary fraction. In this article, I’ll use those formulas to determine the maximum number of digits required by the double-precision (double), single-precision (float), and quadruple-precision (quad) IEEE binary floating-point formats.
The maximum digit counts are useful if you want to print the full decimal value of a floating-point number (worst case format specifier and buffer size) or if you are writing or trying to understand a decimal to floating-point conversion routine (worst case number of input digits that must be converted).
Continue reading “Maximum Number of Decimal Digits In Binary Floating-Point Numbers”
The binary fraction 0.101 converts to the decimal fraction 0.625; the binary fraction 0.1010001 converts to the decimal fraction 0.6328125; the binary fraction 0.00111011011 converts to the decimal fraction 0.23193359375. In each of those examples, the binary fraction converts to a decimal fraction — that is, a terminating decimal representation — that has the same number of digits as the binary fraction has bits.
One digit per bit? We know that’s not true for binary integers. But it is true for binary fractions; every binary fraction of length n has a corresponding equivalent decimal fraction of length n.
This is the reason why you get all those “extra” digits when you print the full decimal value of an IEEE binary floating-point fraction, and why glibc strtod() and Visual C++ strtod() were once broken.
Continue reading “Number of Decimal Digits In a Binary Fraction”
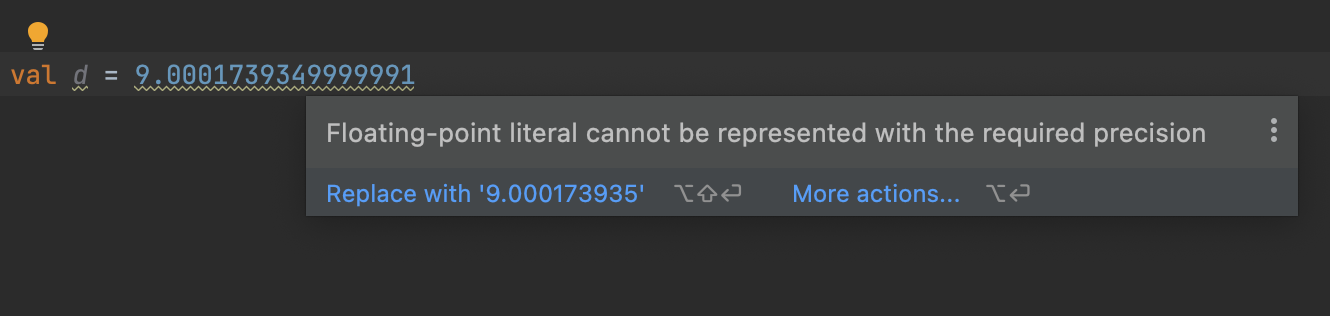
Every double-precision floating-point number can be specified with 17 significant decimal digits or less. A simple way to generate this 17-digit number is to round the full-precision decimal value of the double to 17 digits. For example, the double-precision value 0x1.6d4c11d09ffa1p-3, which in decimal is 1.783677474777478899614635565740172751247882843017578125 x 10-1, can be recovered from the decimal floating-point literal 1.7836774747774789e-1. The extra digits are unnecessary, since they will only take you to the same double.
On the other hand, an arbitrary, arbitrarily long decimal literal rounded or truncated to 17 digits may not convert to the double-precision value it’s supposed to. This is a subtle point, one that has even tripped up implementers of widely used decimal to floating-point conversion routines (glibc strtod() and Visual C++ strtod(), for example).
Continue reading “17 Digits Gets You There, Once You’ve Found Your Way”
How many decimal digits of precision does a binary floating-point number have?
For example, does an IEEE single-precision binary floating-point number, or float as it’s known, have 6-8 digits? 7-8 digits? 6-9 digits? 6 digits? 7 digits? 7.22 digits? 6-112 digits? (I’ve seen all those answers on the Web.)
Continue reading “Decimal Precision of Binary Floating-Point Numbers”
PHP’s base_convert() is a useful function that converts integers between any pair of bases, 2 through 36. However, you might hesitate to use it after reading this vague and mysterious warning in its documentation:
base_convert() may lose precision on large numbers due to properties related to the internal “double” or “float” type used.
The truth is that it works perfectly for integers up to a certain maximum — you just have to know what that is. I will show you this maximum value in each of the 35 bases, and how to check if the values you are using are within this limit.
The 2015 edition of Hour of Code includes a new blocks-based, Star Wars themed coding lesson. In one of the exercises — a simple sprite-based game — you are asked to code a loop that adds 100 to your score every time R2-D2 encounters a Rebel Pilot. But instead of 100, I plugged in a floating-point number; I got the expected “unexpected” results.
Continue reading “An Hour of Code… A Lifelong Lesson in Floating-Point”
I have been writing about the spacing of decimal and binary floating-point numbers, and about how their relative spacing determines whether numbers round-trip between those two bases. I’ve stated an inequality that captures the required spacing, and from it I have derived formulas that specify the number of digits required for round-trip conversions. I have not proven that this inequality holds, but I will prove “half” of it here. (I’m looking for help to prove the other half.)
Continue reading “The Inequality That Governs Round-Trip Conversions: A Partial Proof”
In my article “7 Bits Are Not Enough for 2-Digit Accuracy” I showed how the relative spacing of decimal and binary floating-point numbers dictates when all conversions between those two bases round-trip. There are two formulas that capture this relationship, and I will derive them in this article. I will also show that it takes one more digit (or bit) of precision to round-trip a floating-point number than it does to round-trip an integer of equal significance.
Continue reading “Number of Digits Required For Round-Trip Conversions”
