This is the second of a four part series on “pencil and paper” binary arithmetic, which I’m writing as a supplement to my binary calculator. The first article discusses binary addition; this article discusses binary subtraction.
The pencil-and-paper method of binary subtraction is just like the pencil-and-paper method of decimal subtraction you learned in elementary school. Instead of manipulating decimal numerals, however, you manipulate binary numerals, according to a basic set of rules or “facts.”
Decimal Subtraction
For decimal subtraction, the basic facts are things like 5 – 1 = 4, 9 – 8 = 1, and 18 – 9 = 9. In each case, the answer is a single-digit, nonnegative integer. Most of the facts are “single-digit minus single-digit” problems, but some are “double-digit minus single-digit” problems (the double digits are the numbers 10 through 18). The latter represent cases of borrowing, which is the process by which negative answers are prevented.
Here’s an example of decimal subtraction:

After the points are aligned, subtraction proceeds from right to left. Red marks indicate borrowing. If a non-zero digit is borrowed from, it is crossed out, one is subtracted from it, and the decremented digit is written above it; a 1 is then placed next to the digit in the borrowing position, making it a two-digit number. If a zero digit is borrowed from, the borrow “cascades” until a non-zero digit is found.
Here’s the example again, step-by-step:

- Step 1: 5 – 0 = 5.
- Step 2: Borrow to make 12 – 5 = 7.
- Step 3: Borrow to make 15 – 7 = 8.
- Step 4: Borrow to make 10 – 1 = 9.
Some people refer to this as the “American method” (although this is just one variation of it — see Salman Khan’s video, for example). Whatever your method is though, you can apply it to binary numbers.
Binary Subtraction
For binary subtraction, there are four facts instead of one hundred:
- 0 – 0 = 0
- 1 – 0 = 1
- 1 – 1 = 0
- 10 – 1 = 1
The first three are the same as in decimal. The fourth fact is the only new one; it is the borrow case. It applies when the “top” digit in a column is 0 and the “bottom” digit is 1. (Remember: in binary, 10 is pronounced “one-zero” or “two.”)
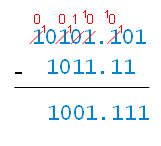
Now let’s subtract 1011.11 from 10101.101, following the same algorithm I used for decimal numbers:
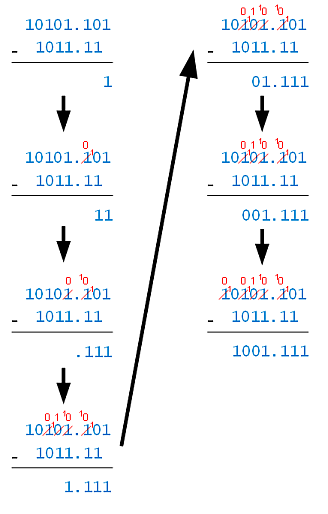
- Step 1: 1 – 0 = 1.
- Step 2: Borrow to make 10 – 1 = 1.
- Step 3: Borrow to make 10 – 1 = 1.
- Step 4: Cascaded borrow to make 10 – 1 = 1.
- Step 5: 1 – 1 = 0.
- Step 6: 0 – 0 = 0.
- Step 7: Borrow to make 10 – 1 = 1.
Since there are lots of 0s in binary numbers, there can be lots of borrows — and lots of messy looking cross-outs.
Checking the Answer
You can check the answer in a few ways. One way is to add the result (1001.111) to the subtrahend (1011.11), and check that that answer matches the minuend (10101.101):

Another way is to convert the operands to decimal, do decimal subtraction, and then convert the decimal answer to binary. 10101.101 = 21.625 and 1011.11 = 11.75, and 21.625 – 11.75 = 9.875. 9.875 = 1001.111, the answer we got using binary subtraction.
You can also check the answer using my binary calculator.
Subtracting a Bigger Number From a Smaller Number
To subtract a bigger number from a smaller number, just swap the numbers, do the subtraction, and negate the result.
Discussion
Notice that I didn’t discuss the number base when describing the algorithm; it is base-independent. Nonetheless, I could have talked about powers of ten and powers of two, and how the process can be visualized by regrouping. My goal was to explain just the mechanized algorithm (presumably you do decimal subtraction mechanically, no longer thinking about why it works).
Subtracting Using Complements
Computers don’t subtract this way; they subtract by adding complements. It’s more efficient. You can do subtraction by complements with pencil-and-paper, but you won’t find it more efficient. (In decimal, you would use nine’s complement or ten’s complement; in binary, you would use ones’ complement or two’s complement.)

SIMPLE & EASY. TOO GOOD.
I was not able to learn binary subtraction without this site thanks a lot.
Now I know.
Very simple and very easy to understand.
Thanks
what will happen if the last digit in the left side is 0..i mean there is nothing left to borrow? is there any rule about it?
@jay ann,
Are you talking about subtracting a bigger number from a smaller number? As I mentioned in the article, just swap the numbers, do the subtraction, and negate the result.
Why 0- 1 =1 in binary
Please explain its theory…soon
@pritam,
0-1 = -1 in binary.
Your method rocks!!!
thanks a lot 🙂 Really helps . Keep the good work going 😀
thanks & thanks a lot I had a problem of subtraction of Binary numbers but fortunately this site helped me a lot,God bless you
11001-101
11001-101=?
It doesn’t work for bot numbers larger than top one.
@Gaspar,
You have to swap the numbers and negate (see section “Subtracting a Bigger Number From a Smaller Number”).
Really amazing stuff, thanks a lot! Simple, easy, and efficient. Understanding your explanation perfectly; you have the right amount of detail.
Thax a lot for clearing my doubts.
I was washaving trouble doing it, but when I read this and took notes I became so good in it.
Thanks so much
Subtraction of larger number from smaller number… I am doing implementation I cannot be sure about when it is big or small…. You have a general algorithm thanks in advance
Thanks, Rick Regan.
Thanks a lot,I’m one of the people who had a problem with subtracting of binary but i must say,you helped me a lot. Keep on the good work,God bless you
thanks so much for the elusive teaching
Your method rocks
thank you so much…!!
only because of u…i m able to learn this !!
thank you so much…god bless you !!
Very easy and nice example. Thnx..just before 1night of exam. This is very help full. Thnx again.
Your examples involves 2 binary numbers, what if the problem involves 3 or 4 binary numbers to be deducted? Thank you
@feb,
Unless I misunderstand your question, just subtract them in sequence. So for example, in decimal, 10 – 2 – 1 – 3: 10 – 2 = 8; 8 – 1 = 7; 7 – 3 = 4.
What if you had, for example 10010 take 100? How would you carry the 1’s?
@Mash,
The borrow cascades until you hit a 1.
Let’s look at your example (sorry, I will have to do in words — no graphics). The first two steps are straightforward:
At this point, you try to subtract from a 0, so you have to go left, where you find a 0. You then go left again, where you find a 1. You cross off the 1 (make it a 0) and make the place to its right 10. But then you cross out the 10 and make it a 1, borrowing to make the original place 10. So at the original place you do 10 – 1 = 1, then go left and do 1 – 0 = 1. This is the result:
Hi!^_^ ..how can you solve this..1001-1111?
@just,
Swap the numbers and negate the result (see section “Subtracting a Bigger Number From a Smaller Number”.)
From which end the Borrow process should be followed ? Is it from right end or left end of the Binary number?Please explain.
@Ashok,
Borrowing is always from the left (see the diagram “Steps of Binary Subtraction”).
O M G! Thanks to this! I undertstand it well.
O M G! Thanks Rick!
I just want to ask if the last digit is 0? what will i do?
@Samantha,
I don’t understand your question — please give me an example.
well explained
Thank you so much, Rick.
In my engineering class we have to learn about basic operations with binary numbers and the material provided was not very explicit at all (online classes).
Found your website and you make it soooo easy.
Oh, and your calculator provided big help to check my results.
A 1111101000 thanks. 🙂
I really thank this site because without it I can’t study binary calculations .
I really thank this site because without it I can’t study binary calculations .In this site I trying a lot of questions .
Thanks a lot Rick. It’s a vey simple and easy method. By this i just binary subtraction, now i am moving to your next article. Thanks again. 🙂
you make it so easy.. 🙂 but tell me one thing that if the last number of question is 0 than how to borrow 1 for the right side number for example
question is: 110110 from 001110 plzz tell me the answer soon..
@afifa,
You are trying to subtract a bigger number from a smaller one — just swap them and tack a minus sign onto the answer.
Thanks u very much, these are all simple method for learners and teaching
@vedavyas, you can check which of the numbers is the bigger one by simply testing which one starts first (with “1”), from left to right. For example, let’s say you have two numbers in a form:
00001???? (four zeros, then 1, then some digits)
00000???? (four zeros, then 0, then some digit)
In both numbers, all four highest positions (powers of 2) are the same: 0, so they cannot differ by those. But Then we have the fifth position (counting from left) where the difference is, and this is the *most significant* difference! (because it is also the most significant digit). In the first number, there’s “1” present at this position, which tunrs on this particular power of 2 (includes it into the number). But in the second number, there’s “0” at that position, which means this power of 2 is *not* included. Even if all the “?”s in the first number were set to “0”, and all “?”s in the second number were set to “1”s, the first number would still be greater by 1 from the bottom number, because the most significant bit DOUBLES whatever could be covered by the combination of “?” bits below it. So all the “?”s set in the bottom number would still be that power of 2 *less one*; in other words, no matter how much it tries, it can *never* catch up with the number which has “1” at the position next to the row of “?”s.
So the simplest way to find out which number is the greater, is to scan both numbers from left to right, bit by bit (pairwise), and which ever will start with “1” as first, is the greater.
@SasQ,
Thanks for that. I guess I never really described how to determine the bigger number when looking at them in binary.
@Rick,
m still confuse i can’t understand :/ plzz explain me 🙁
@affa,
Just subtract 001110 from 110110, instead of subtracting 110110 from 001110. Then, just prepend a minus sign to your answer. It’s just like in decimal: 3-4 is the same as -(4-3).
Thank you I understand now 🙂
Gud easy learning.