Numbers Greater Than DBL_MAX Should Convert To DBL_MAX When Rounding Toward Zero

By Rick Regan  April 21st, 2024

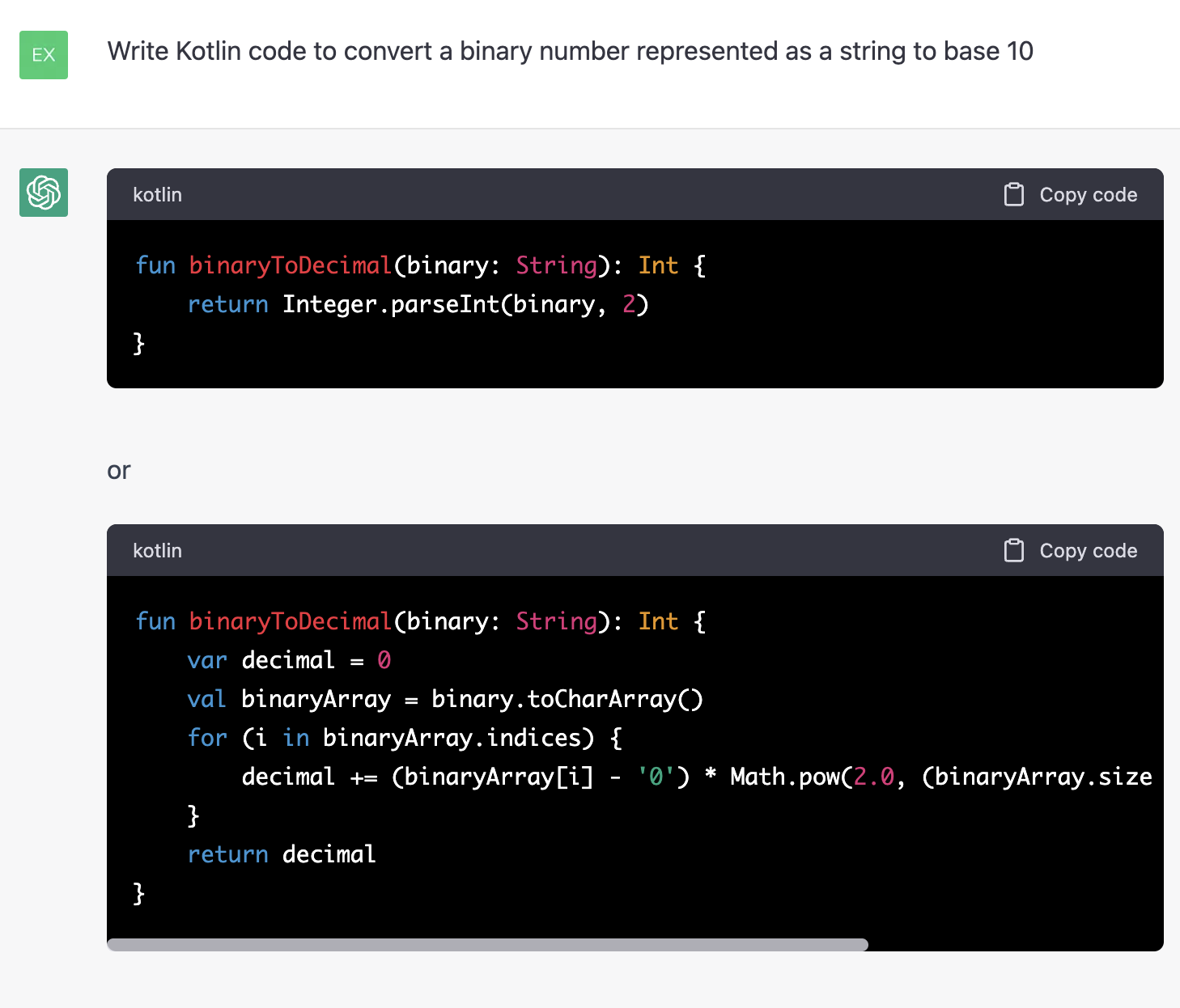
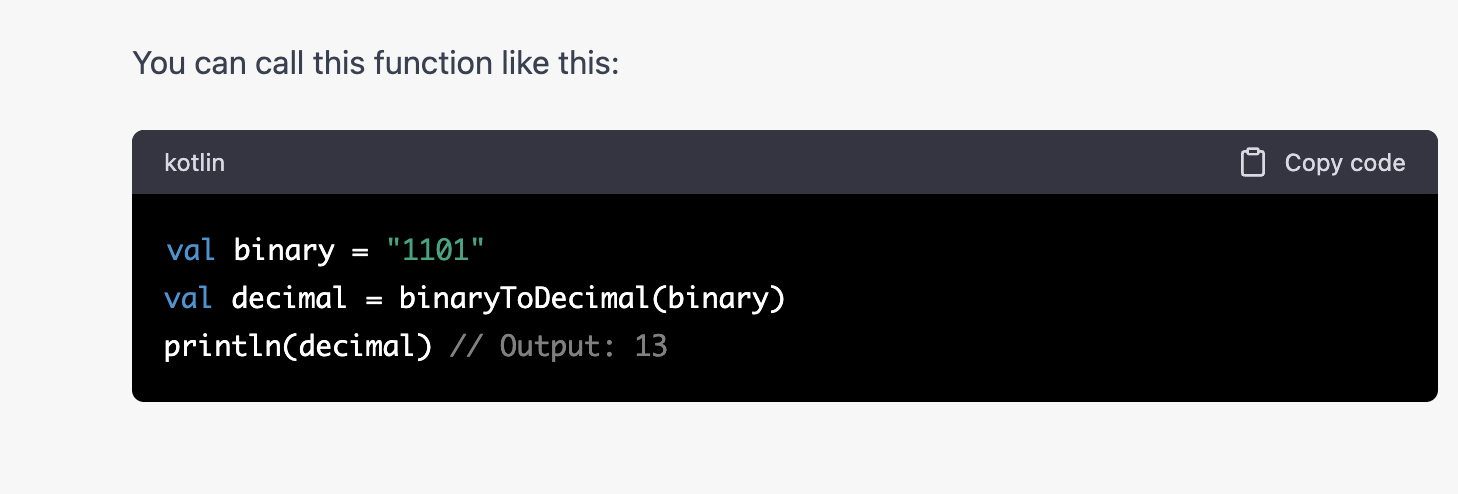
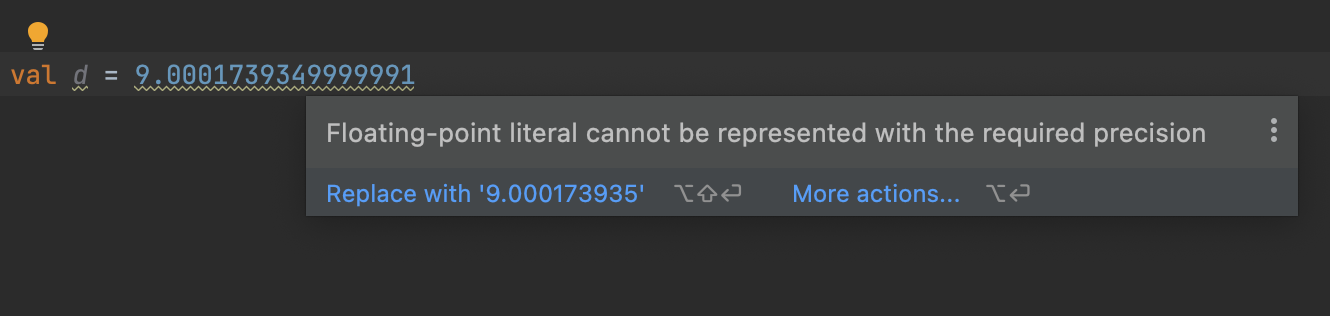
I was testing David Gay’s most recent fixes to strtod() with different rounding modes and discovered that Apple Clang C++ (Xcode) and Microsoft Visual Studio C++ produce incorrect results for round towards zero and round down modes: their strtod()s convert numbers greater than DBL_MAX to infinity, not DBL_MAX. At first I thought Gay’s strtod() was wrong, but Dave pointed out that the IEEE 754 spec requires such conversions to be monotonic.

Continue reading “Numbers Greater Than DBL_MAX Should Convert To DBL_MAX When Rounding Toward Zero”

NaNs, Infinities, and Negative Numbers In Loan Calculators

By Rick Regan  February 6th, 2024

I’ve encountered several NaNs over the years in the normal course of using various websites and apps. I’ve only documented two of them: one in a media player, and one in a podcast app. I recently ran into another one using a loan calculator website. Rather than reporting on just that one, I decided to look for more and report on anything I found all at once.

I found many more errors — NaNs, but also infinites, negative numbers, and one called “incomplete data”, whatever that means — all on websites within the top Google search results for “loan calculator”. All I had to do to elicit these errors was to enter large numbers. (And in one case, simply including a dollar sign.) All of the errors arise from the use of floating-point arithmetic combined with unconstrained input values. Some sites even let me enter numbers in scientific notation, like 1e308, or even displayed them as results.

Floating point error in loan calculator

Continue reading “NaNs, Infinities, and Negative Numbers In Loan Calculators”

Incorrect Hexadecimal to Floating-Point Conversions in David Gay’s strtod()

By Rick Regan  January 30th, 2024

I wrote about Visual C++ incorrectly converting hexadecimal constants at the normal/subnormal double-precision floating-point boundary. It turns out that David Gay’s strtod() also has a problem with the same inputs, converting them all to 0 instead of 0x1p-1022.

I have emailed Dave Gay to report the problem; I will update this post when he responds.

Update 2/28/24

The bug is now fixed (after several iterations) and is available in netlib. Thanks to Dave Gay for the quick turnaround.

Typically, I use Gay’s strtod() to check the outputs of other conversion routines (examples: Visual C++, GCC and GLIBC, PHP). In this case, the roles were reversed: I used another C implementation, Apple Clang C++ , to check Gay’s strtod().

Incorrect Hexadecimal to Floating-Point Conversions in Visual C++

By Rick Regan  January 26th, 2024

Martin Brown, through a referral on his Stack Overflow question, contacted me about incorrect hexadecimal to floating-point conversions he found in Visual C++, specifically conversions using strtod() at the normal/subnormal double-precision floating-point boundary. I confirmed his examples, and also found an existing problem report for the issue. It is not your typical “off by one ULP due to rounding” conversion error; it is a conversion returning 0 for a non-zero input or returning numbers with exponents off by binary orders of magnitude.

Continue reading “Incorrect Hexadecimal to Floating-Point Conversions in Visual C++”

ChatGPT Will Never Write For Exploring Binary

By Rick Regan  September 16th, 2023

I got an unsolicited email from a company offering to write AI (ChatGPT) generated articles for my site. This is the snippet they sent of their sample article:

Mastering Decimal, Binary, & Two’s Complement Conversion

In the digital world, understanding numerical notations like decimal, binary, and two’s complement can provide a substantial advantage and presents opportunities for improved problem-solving. The journey starts with the basic foundation of decimal …

I did not click through the tracking link to get the rest of the article but it looks like the generic fluff ChatGPT wrote when I asked it about Exploring Binary. It’s worse than fluff actually; I don’t see how knowing numerical notations helps with problem solving.

If you’ve read anything on this site you’d know immediately that I didn’t write that. Will AI ever be able to write an article indistinguishable from one of my own? I don’t think so.

Jetpack Compose Byte Converter App: 2022 Version

By Rick Regan  August 12th, 2022

I wrote a simple byte to decimal converter app less than two months into starting to learn Jetpack Compose. Now that I have more experience with Compose — in developing a real app and by participating on the #compose channel on Slack (login required) — I wanted to update this demo app to reflect my current understanding of best practices.

Continue reading “Jetpack Compose Byte Converter App: 2022 Version”

Anomalies In IntelliJ Kotlin Floating-Point Literal Inspection

By Rick Regan  July 19th, 2022

IntelliJ IDEA has a code inspection for Kotlin that will warn you if a decimal floating-point literal exceeds the precision of its type (Float or Double). It will suggest an equivalent literal (one that maps to the same binary floating-point number) that has fewer digits, or has the same number of digits but is closer to the floating-point number.

Screenshot in IntelliJ IDEA of hovering over a flagged 17-digit literal with a suggested 10-digit replacement
Hovering over a flagged 17-digit literal suggests a 10-digit replacement.

For Doubles for example, every literal over 17-digits should be flagged, since it never takes more than 17 digits to specify any double-precision binary floating-point value. Literals with 16 or 17 digits should be flagged if there is a replacement that is shorter or closer. And no literal with 15 digits or fewer should ever be flagged, since doubles have of 15-digits of precision.

But IntelliJ doesn’t always adhere to that, like when it suggests an 18-digit replacement for a 13-digit literal!

Screenshot of IntelliJ IDEA suggesting an 18-digit replacement for a 13-digit literal
An 18-digit replacement suggested for a 13-digit literal!

Continue reading “Anomalies In IntelliJ Kotlin Floating-Point Literal Inspection”

Showing n! > 2n When n Is A Power of Two

By Rick Regan  August 22nd, 2021

Which is bigger, 64! or 264? 64! is, because it follows from a proof by induction for any integer n greater than or equal to 4. It’s also easy to just reason that 64! is bigger: 264 is 64 factors of 2, whereas 64! has 64 factors, except all but one of them (1) are 2 or greater.

When I saw this problem though I wondered if I could solve it in another way: Could the factors of two alone in 64! be greater than 264? As it turns out, almost.

Continue reading “Showing n! > 2n When n Is A Power of Two”

Hexadecimal Numbers: Uppercase or Lowercase?

By Rick Regan  June 29th, 2021

Do you prefer hexadecimal numbers written with uppercase letters (A-F) or lowercase letters (a-f)?

For example, do you prefer the integer 3102965292 written as B8F37E2C or b8f37e2c? Do you prefer the floating-point number 126.976 written as 0x1.fbe76cp6 or 0x1.FBE76Cp6?

I ran this poll on my sidebar, and after 96 responses, about 70% are “prefer uppercase” and about 9% are “prefer lowercase”. What do you think? (For the “depends on context” answer I meant things other than numeric values, like the memory representation of strings. However, for the purposes of this article, please answer with just numeric values in mind.)

Continue reading “Hexadecimal Numbers: Uppercase or Lowercase?”

Copyright © 2008-2025 Exploring Binary

Privacy policy

Powered by WordPress

css.php