Numbers are entered into computers as strings of text. These strings are converted to binary, into the numeric form understood by the computer’s hardware. Numbers with a decimal point — numbers we think of as real numbers — are converted into a format called binary floating-point. The procedure that converts decimal strings to binary floating-point — IEEE double-precision binary floating-point in particular — goes by the name strtod(), which stands for string to double.
Converting decimal strings to doubles correctly and efficiently is a surprisingly complex task; fortunately, David M. Gay did this for us when he wrote this paper and released this code over 20 years ago. (He maintains this reference copy of strtod() to this day.) His code appears in many places, including in the Python, PHP, and Java programming languages, and in the Firefox, Chrome, and Safari Web browsers.
I’ve spent considerable time reverse engineering strtod(); neither the paper nor the code are easy reads. I’ve written articles about how each of its major pieces work, and I’ve discovered bugs (as have a few of my readers) along the way. This article ties all of my strtod() research together.
strtod()’s Raison D'être
strtod() is designed to produce correctly rounded conversions, that is, convert any decimal string to its nearest double-precision binary floating-point number. This could be done quite simply if performance weren’t an issue: arbitrary-precision integer division would do the trick. But arbitrary-precision division is expensive. Enter David Gay’s strtod(). It uses IEEE floating-point arithmetic when it can, and uses arbitrary-precision arithmetic — not full-blown division though — only when necessary. (Some conversions will always require arbitrary-precision — there’s no getting around that. My article “Decimal to Floating-Point Needs Arbitrary Precision” will help you understand why.)
Paths Through strtod()
There are three basic paths that a conversion can take through strtod(): the fast path, for decimal strings that are short enough and have exponents that are small enough; the correction loop, for decimal strings that don’t qualify for the fast path; and bigcomp, for long decimal strings that can’t be resolved by the correction loop because they are nearly halfway between two floating-point numbers. The fast path requires only IEEE arithmetic; the correction loop and bigcomp require IEEE and arbitrary-precision arithmetic.
All paths require the decimal input to be parsed into two components: an integer, representing the significant digits, and a power of ten, representing the placement of the decimal point. For example, 1.23456789012345e36 is parsed into 123456789012345 and 1022, and 3.14159 is parsed into 314159 and 10-5.
Here’s an overview of the flow:
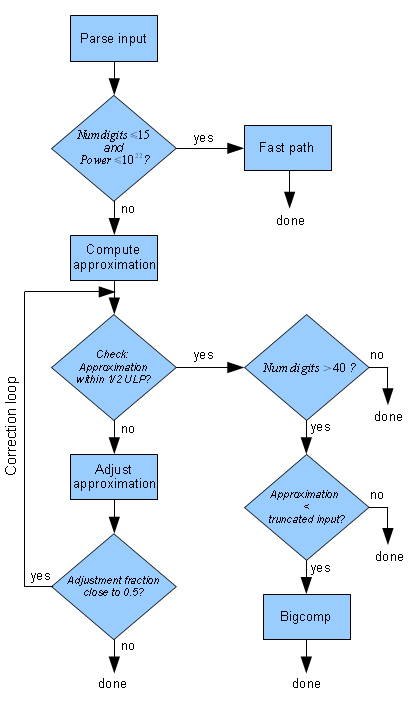
strtod() uses its own arbitrary-precision integer implementation. It manipulates its floating-point result by accessing its underlying representation through a union of a double and two 32-bit integers.
Fast Path
The fast path applies to decimal strings of 15 significant digits or less with a power of ten exponent that has an absolute value of 22 or less (all powers of ten are treated as nonnegative powers of ten). These types of inputs can be correctly rounded with a single IEEE floating-point multiplication or division. For example, 1.23456789012345e36 is converted with 123456789012345 * 10000000000000000000000, and 3.14159 is converted with 314159/100000. This works because those operands are exactly representable in floating-point.
(See my article “Fast Path Decimal to Floating-Point Conversion” for details.)
Correction Loop
The correction loop is required for any input that does not qualify for the fast path; this occurs when either the significant digits integer or nonnegative power of ten or both are not exactly representable in floating-point. (An IEEE floating-point multiplication or division cannot guarantee a correctly rounded result if its operands are already rounded.) For example, 6.2187331579177550499956283 has too many digits, and 163.118762e+109 has a power of ten that’s too big.
For these inputs, strtod() computes an initial floating-point approximation and then uses the loop to check, and if necessary, correct it. IEEE arithmetic is used to calculate the approximation, arbitrary-precision arithmetic is used to check it, and IEEE arithmetic is used to correct it. The majority of inputs require only one pass of the loop.
(See my article “Properties of the Correction Loop in David Gay’s strtod()” for details.)
Approximation
For the approximation, strtod() uses only the first 16 significant digits of the input, and computes the power of ten using binary exponentiation. The inaccuracies introduced here could make the approximation differ from the correct answer by 10 ULPs or so.
(See my article “strtod()’s Initial Decimal to Floating-Point Approximation” for details.)
Check
For the check, strtod() compares the decimal input to the binary approximation to see if they are within one-half of a ULP of each other. The check is made in arbitrary-precision integer arithmetic, using scaled versions of those three values.
(See my article “Using Integers to Check a Floating-Point Approximation” for details.)
Adjustment
strtod() computes an adjustment which itself is an approximation to the distance between the approximation and the correct result. It adds it to or subtracts it from the approximation, as required. If the adjustment contains a fractional portion that is close to 0.5, the loop is repeated; the approximation is rechecked and adjusted again, if necessary.
(See my article “Adjusting the Floating-Point Approximation in strtod()” for details.)
Bigcomp
Bigcomp is an optimization used to reduce arbitrary-precision integer overhead when checking long decimal inputs. It truncates long decimal strings and uses the truncated value in the correction loop. This truncation gives smaller integers, but it can lead to cases where the approximation check cannot decide between adjacent floating-point values. When that happens, the correction loop is exited, and the bigcomp() function is invoked to choose the correct value.
bigcomp(), interestingly, decides which of two neighboring floating-point values is correct by doing a floating-point to decimal conversion. It converts the midpoint of the two values to a string, and then compares that to the input string. From that it can decide to which side the decimal input lies.
(See my article “Bigcomp: Deciding Truncated, Near Halfway Conversions” for details.)
Configuring strtod()
strtod() is written in C and lives in a file called dtoa.c. (This file also contains the dtoa() function — double to ASCII string.) In that file are flags that allow strtod() to be configured. strtod() supports three floating-point architectures (IEEE, IBM, and yes, VAX) and four rounding modes (round-to-nearest, round toward positive infinity, round toward negative infinity, and round toward zero). It can also convert hexadecimal floating-point constants.
Every copy of strtod() I’ve seen in use is configured for IEEE arithmetic and round-to-nearest rounding. To use IEEE arithmetic, you need to “#define” the flag IEEE_8087. In addition, on processors with an x87 FPU, you must set the precision to 53 bits (e.g. on Windows, _controlfp_s(&cur_cw,_PC_53,MCW_PC)), because extended-precision can produce incorrect results.
(There are many more flags; see the code for details.)
Bugs in strtod()
Here I’ll highlight some recent (within the last three years) bugs in strtod() and related decimal to floating-point conversion routines.
Buffer Overflow
This is the bug that got me interested in strtod(). I had been studying the decimal to floating-point conversion routines of gcc and glibc when this security flaw became big news. I was struck by how many projects used it, and how such a well-worn piece of code could still have major bugs.
strtod() caused a buffer overflow when given extremely long decimal inputs. This affected all of the many users of strtod(), including Mozilla, Chrome, and Mac OS.
Infinite Loop
PHP’s and Java’s implementations of strtod() both had serious bugs that were discovered last year; in both cases, their correction loops never terminated! I discovered the PHP bug, which was due to the use of a very old copy of David Gay’s code. Java’s bug was discovered by a reader; it was due to a problem introduced when strtod() was “translated” from C to Java.
You can read about the PHP bug here:
- “PHP Hangs On Numeric Value 2.2250738585072011e-308”
- “Why “Volatile” Fixes the 2.2250738585072011e-308 Bug”
- “A Better Fix for the PHP 2.2250738585072011e-308 Bug”
You can read about the Java bug here:
- “Java Hangs When Converting 2.2250738585072012e-308”
- “A Closer Look at the Java 2.2250738585072012e-308 Bug”
Incorrect Conversions
These articles describe bugs that caused strtod() to do incorrect conversions:
- “Incorrect Directed Conversions in David Gay’s strtod()”
- “A Bug in the Bigcomp Function of David Gay’s strtod()”
- “Quick and Dirty Floating-Point to Decimal Conversion” (Scroll down to the section marked “Endnote” to read about the bug.)
These articles also describe bugs that caused incorrect conversions, but they are Java-specific, and not strtod() per se:
- “Incorrectly Rounded Subnormal Conversions in Java”
- “Nondeterministic Floating-Point Conversions in Java”
(I found some of the above bugs and readers found others.)
Suggested Improvements To strtod()
Here are ways strtod() could be improved (some of these are my ideas; some are my readers’ ideas):
- It could extend the fast path to include most 16-digit numbers, increasing the number of fast path cases eightfold (see my article “Fast Path Decimal to Floating-Point Conversion”).
- It could convert large integers from their big integer binary representation, avoiding the overhead and complexity of the correction loop (see my article “A Better Way to Convert Integers in David Gay’s strtod()”).
- It could improve its performance for long inputs if it raised the cutoff for bigcomp() from 40 digits to at least 80 digits (see my article “Bigcomp: Deciding Truncated, Near Halfway Conversions”).
- It could avoid potential infinite loops by limiting the number of times through the correction loop (see my article “Properties of the Correction Loop in David Gay’s strtod()”).
(This section was added 9/20/13.)
And For Those That Don’t Use strtod()?
Some programming environments don’t use David Gay’s strtod(); Visual C++, gcc, glibc, and SQLite are examples. I have found incorrect conversions in each:
- “Incorrectly Rounded Conversions in Visual C++”
- “Incorrectly Rounded Conversions in GCC and GLIBC”
- “Incorrect Decimal to Floating-Point Conversion In SQLite”
- “Double Rounding Errors in Floating-Point Conversions”
Discussion
I want to end with a few additional points:
- My description of strtod() focused on normal numbers rounded under round-to-nearest rounding. I did not discuss details of special cases, like subnormal numbers, overflow, and underflow.
- If your project uses strtod(), make sure to keep it up-to-date.
- I wonder: who needs to specify a constant to thousands, hundreds, or even tens of digits? A large part of strtod()’s complexity is due to long inputs. Why do we allow them?
- Next time you type a floating-point constant into your code, be thankful you didn’t have to convert it yourself!
Acknowledgements
Thanks to Mark Dickinson for answering my questions and for his instructive comments inside Python’s copy of strtod(); thanks to whoever wrote Java’s FloatingDecimal class, also useful for its commentary; and thanks to Dave Gay, for answering my questions and for his quick turnaround on strtod() patches.

Hi, Rick. Great conclusion to a great series!
What can I do to convince you to exert your testing skills on the new decimal-to-binary function in Frama-C’s front-end?
Testing it is as easy as getting a relatively recent OCaml (at least 3.10.2 for most Unices including Mac OS X Leopard-Lion, 4.00.1 for Mountain Lion), getting the source for Frama-C Oxygen from http://frama-c.com/install-oxygen-20120901.html , compiling, and typing a small C program such as:
float f = 3.1415927f;
double d = 2.7182818284590452;
The command below prints the values converted in hexadecimal:
frama-c -warn-decimal-float all t.c
t.c:1:[kernel] warning: Floating-point constant 3.1415927f is not represented exactly. Will use 0x1.921fb60000000p1
t.c:2:[kernel] warning: Floating-point constant 2.7182818284590452 is not represented exactly. Will use 0x1.5bf0a8b145769p1
Hi Pascal,
Thanks. With this article I was planning to put decimal to binary conversion to rest so that I could continue with binary to decimal conversion.
Perhaps you could do some stress testing by running your code against Gay’s? That’s how I found the incorrect conversions in Visual C++, for example. Also, you could try some of the “hard” conversion examples I’ve discussed in some of my articles.
Good luck!
Hello again,
Your suggested testing methodology was the one I had already used.
I tried the constants 2.2250738585072012e-308
and 2.2250738585072011e-308 first as these are practical
worst cases for the naive implementation (a really naive implementation,
like mine is, is even slower on 1.0e-500, or 1.0e1000, but the programmer
cannot claim that it is useful for him to write such a double-precision
constant).
And I randomly generated some decimal representations of numbers
that were nearly in-between two doubles.
However, a random code review identified two stupid bugs in my conversion
function:
http://blog.frama-c.com/index.php?post/2012/11/19/Funny-floating-point-bugs-in-Frama-C-Oxygen-s-front-end
Password: decimal
Pascal,
I haven’t tried “zeros with exponents” as in your article’s examples.
Hi,
will you publish a fixed version of dtoa.c which I could include in my operating system (MirBSD)?
I wonder a bit about the modes. We already set the i387 to 53 bits mode (unlike e.g. Linux and more recent OpenBSD versions), but the user is permitted to change the FPU flags (both precision and rounding modes). Do we just specify that calling dtoa/strtod is forbidden if they do that, or should we save+change and restore the FPU state on function entry/exit (which could surprise signal handlers that expect the program-global state… and blocking signals is also not a nice thing to do…)?
@mirabilos,
David Gay maintains dtoa.c and he keeps it current, with fixes to bugs I and others have reported. It’s at http://www.ampl.com/netlib/fp/ . (None of my “suggested improvements” were ever implemented.)
You’d need to switch to “53-bit” mode for strtod(). Here’s the relevant comment in dtoa.c:
/* On a machine with IEEE extended-precision registers, it is
* necessary to specify double-precision (53-bit) rounding precision
* before invoking strtod or dtoa. If the machine uses (the equivalent
* of) Intel 80×87 arithmetic, the call
* _control87(PC_53, MCW_PC);
You asked “who needs to specify a constant to thousands, hundreds, or even tens of digits?”. One reason is that some numerical methods involve coefficients which are
specified as rationals with quite large numerator/denominator. For example, a recent
paper by Boscarino (Applied Numerical Mathematics volume 59, pages 1515-1528)
includes this coefficient::
a41 = 1103202061574553405285863729195740268785131739395559693754 / 9879457735937277070641522414590493459028264677925767305837
So, how do we convert this bignum-rational-number into a floating-point number,
and get the latter into a table-of-coefficients in our {C,C++,Fortran,Perl,…} program?
In practice I can see two fairly easy ways:
(a) find a software environment with a bignum-arithmetic package,
and let it do the work, then print out the floating-point result and copy the
resulting literal into our {C,C++,Fortran,Perl,…} program, or
(b) have the {C,C++,Fortran,Perl,…} program do the division itself by writing
code like this:
const double a_41 = 1103202061574553405285863729195740268785131739395559693754.0 / 9879457735937277070641522414590493459028264677925767305837.0;
Either way, _some_ piece of software is going to have to turn these (bignum)
numerator and denominator into something that the computer knows how to
divide. While this _could_ be done with decimal floating-point, I think doing it
with binary is not unreasonable, and either (a) or (b) provides a use case to
answer your question.
Erm, Jonathan, if you write it like this into the source code, the program is *not* going to do it by itself, but the (cross-)compiler is calculating the value at compile time (possibly with loss of precision, e.g. if you build on a 32-bit soft-float ARM CPU for a CPU with 128-bit long doubles) and inserting the result into the program directly. (No way around this with “const” in use, even – optimisation will always result in this.)
@mirabilos: I was writing for the compile-on-same-system case. As you point out,
cross-compiling is a whole other can of worms.