Nonstandard Names for The Powers of Two

Now that you know how the powers of two are named, lets look at other, nonstandard ways to name them. You will see these names on the internet as well as in books. We will not use them on this site other than in this article, and we only discuss them here to make you aware of their use. As a by-product of this discussion, you may gain some insight into the nature of the powers of two. But beware — you may become confused as well!

Other Names for The Powers of Two

Sometimes the terms integer powers of two and integral powers of two are used instead of, just simply, powers of two. The words “integer” and “integral” in this case qualify the word “powers,” which is unnecessary because the definition of the powers of two implies integer powers. In fact, it’s more than unnecessary, it’s confusing; some people use these terms to mean the nonnegative powers of two, as you’ll see below.

Other Names for The Nonnegative Powers of Two

Sometimes the terms integer powers of two and integral powers of two are used for the nonnegative powers of two. The words “integer” and “integral” in this case qualify the phrase “powers of two,” meaning that the powers of two in question are integers and not fractions.

You might see the terms nonnegative integer powers of two and nonnegative integral powers of two. These are not so much confusing as they are redundant, with integer being implied in the definition.

Another term you might see describing the nonnegative powers of two is the whole powers of two. Technically, this term is ambiguous, because it could mean either whole powers or whole powers of two; that is, powers that are whole numbers (0, 1, 2, …) or powers of two that are not fractional. It turns out to be the same set of numbers in either case, but the more consistent interpretation is that the powers are whole.

Also, as we pointed out in the standard definition, the nonnegative powers of two are commonly referred to simply as the powers of two.

Other Names for The Positive Powers of Two

You might see the terms positive integer powers of two and positive integral powers of two. As we’ve said, integer is redundant since it’s implied in the definition.

Another term for the positive powers of two is the natural powers of two. A natural number is a positive integer, so a natural power is the same thing as a positive power.

Also, as we pointed out in the standard definition, the positive powers of two are commonly referred to simply as the powers of two.

Other Names for The Negative Powers of Two

Like the other terms above, there are the redundant variations for the negative powers of two: negative integer powers of two and negative integral powers of two. But there are also several more interesting terms that try to convey the inverse relationship between the negative powers of two and the positive powers of two:

The inverse powers of two
The inverted powers of two
The reciprocal powers of two
The fractional powers of two

In these terms, “powers of two” is used implicitly to mean just the positive powers of two (see alternate definitions of the powers of two.). Accordingly, the words inverse, inverted, reciprocal, and fractional qualify the entire phrase “powers of two.”

These terms indicate that the positive powers of two — the ones you know and love — are now just denominators of unit fractions.

The Powers of One-Half

A seemingly unrelated term substituting for the negative powers of two is the powers of one-half. The powers of one-half, written in terms of proper fractions, is the set

$\mbox{\footnotesize{\left\{\left(\frac{1}{2}\right )^1, \left(\frac{1}{2}\right )^2, \left(\frac{1}{2}\right )^3, \left(\frac{1}{2}\right )^4, \left(\frac{1}{2}\right )^5, \left(\frac{1}{2}\right )^6, \ldots} \right\}}}$ or

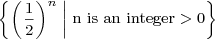$\mbox{\footnotesize{\displaystyle \left\{ {\left(\frac{1}{2}\right )^n \biggm\vert \text{n is an integer} > 0} \right\}}}$ .

You can see these are the same as the negative powers of two since

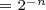${\footnotesize{{\left(\frac{1}{2}\right)}^n = \frac{1^n}{2^n} = \frac{1}{2^n}}$ $\mbox{\footnotesize{= 2^{-n}}}$ .

In terms of decimals, the powers of one-half are

$\mbox{\footnotesize{\left\{ {0.5^1, 0.5^2, 0.5^3, 0.5^4, 0.5^5, 0.5^6, \ldots} \right\}}}$ or

$\mbox{\footnotesize{\displaystyle \left\{ {0.5^n \mid \text{n is an integer} > 0} \right\}}}$ .

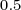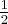Using the same math as above, you can see these are the same as the negative powers of two since $\mbox{\footnotesize{0.5}}$ = $\footnotesize{\frac{5}{10}}$ = $\footnotesize{\frac{1}{2}}$ .

While technically they should be called the positive powers of one-half, you can see why no one bothers with this qualification. That’s because you would not need the term negative powers of one-half — that’d be just a more cumbersome way to describe the positive powers of two! Here’s the math:

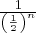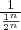${\footnotesize{{\left(\frac{1}{2}\right)}^{-n}}$ = $\frac{1}{\left(\frac{1}{2}\right)^{n}}}$ = $\frac{1}{\frac{1^n}{2^n}}}$ = $\frac{1}{\frac{1}{2^n}}}$ = $\mbox{\footnotesize{2^n}}$ .

One potential problem with this term is that “a power of one-half” might be confused with raising a number to a power that is one-half, that is, taking its square root.

And if That Weren’t Enough…

For all these different terms — the standard terms, the nonstandard ones described above, and even some rarely used terms we haven’t mentioned — there are common spelling variations. You might want to take this into account if you decide to search the web for related information. For example, use numerals as well as number words: powers of 2, powers of 1/2, etc. Also, be aware of variations that add or drop a hyphen: non-negative powers of two, non-positive powers of two, powers of one half, etc.

Alternate Naming for The Powers of Two and Its Subsets

From this sea of largely incompatible terms I’ve managed to cherry-pick a few to create a reasonable alternative to the standard names:

Nonstandard naming of the powers of two and its subsets.

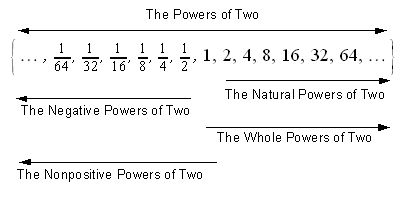
This is equivalent to the standard definition, except that the subset names are less symmetric. I’m not recommending that you use it, but I wouldn’t object if you did.

2 comments

David Eisner says:

February 3, 2011 at 5:16 pm

The words “integer” and “integral” in this case qualify the word “powers,” which is unnecessary because the definition of the powers of two implies integer powers

Can’t an argument be made that this is not redundant? In mathematical parlance, when one raises a number to a given “power”, that power need not be an integer. For example, 2 raised to the power of 1/2 is the square root of two. (I know *you* know this)

So “integral powers of two” could be interpreted to mean the set {2^a | a is an integer}, as opposed to {2^a | a is a real number}.

The problem is that “power” is an overloaded word. In the sentence “Sixty-four is indeed a power of two. It is two raised to the sixth power”, the word “power” refers to 2^6 in the first instance, and to 6 in the second.
Rick Regan says:

February 3, 2011 at 5:43 pm

David,

You can make that argument, but in my article “A Standard Definition of The Powers of Two” I make a case for the term “powers of two” implying integer exponents only. So from the point of view of my definition, it is redundant.

And yes, I agree that “power” is an overloaded word.

Comments are closed.