Articles with the ‘Exponents’ Tag - Exploring Binary

Powers Of Two In The Josephus Problem

By Rick Regan July 24th, 2009

Pradeep Mutalik of The New York Times recently blogged about a puzzle that is an instance of the Josephus Problem. The problem, restated simply, is this: there are n people standing in a circle, of which you are one. Someone outside the circle goes around clockwise and repeatedly eliminates every other person in the circle, until one person — the winner — remains. Where should you stand so you become the winner?

Here’s an example with 13 participants:

Alternating Elimination with 13 people, order of elimination shown in red (winner is person 11)

As Pradeep and his readers point out, there’s no need to work through the elimination process — a simple formula will give the answer. This formula, you won’t be surprised to hear, has connections to the powers of two and binary numbers. I will discuss my favorite solution, one based on the powers of two.

Continue reading “Powers Of Two In The Josephus Problem”

Nines in Binary

By Rick Regan June 10th, 2009

I discovered a cool property of positive integers of the form 10ⁿ-1, that is, integers made up of n digits of 9s: they have binary representations that have exactly n digits of trailing 1s. For example, 9,999,999 in decimal is 100110001001011001111111 in binary.

The property is interesting in and of itself, but what is more interesting is the process I went through to discover it. It’s a small-scale example of experimental mathematics: I observed something interesting, experimented to collect more data, developed a hypothesis, and constructed a proof.

Continue reading “Nines in Binary”

Elements of Binary in the NCAA Basketball Tournament

By Rick Regan March 11th, 2009

If you’re a sports fan, you think of basketball when you see this:

Diagram of the NCAA Basketball Tournament — Basketball or Binary?

If you’re like me, you also think of powers of two, binary trees, logarithms, laws of exponents, geometric sequences, geometric series, and Bernoulli trials — in short, the elements of binary numbers, binary code, and binary logic.

I hope you’re thinking: “wow — all that math stuff I hated actually has a practical use!”

Continue reading “Elements of Binary in the NCAA Basketball Tournament”

Print Precision of Floating-Point Integers Varies Too

By Rick Regan February 11th, 2009

Recently I showed that programming languages vary in how much precision they allow in printed floating-point fractions. Not only do they vary, but most don’t meet my standard — printing, to full precision, decimal values that have exact floating-point representations. Here I’ll present a similar study for floating-point integers, which had similar results.

Continue reading “Print Precision of Floating-Point Integers Varies Too”

Print Precision of Dyadic Fractions Varies by Language

By Rick Regan January 30th, 2009

Interestingly, programming languages vary in how much precision they allow in printed floating-point fractions. You would think they’d all be the same, allowing you to print as many decimal places as you ask for. After all, a floating-point fraction is a dyadic fraction; it has as many decimal places as it has bits in its fractional representation.

Consider the dyadic fraction 5,404,319,552,844,595/2⁵³. Its decimal expansion is 0.59999999999999997779553950749686919152736663818359375, and its binary expansion is 0.10011001100110011001100110011001100110011001100110011. Both are 53 digits long. The ideal programming language lets you print all 53 decimal places, because all are meaningful. Unfortunately, many languages won’t let you do that; they typically cap the number of decimal places at between 15 and 17, which for our example might be 0.59999999999999998.

Continue reading “Print Precision of Dyadic Fractions Varies by Language”

What Powers of Two Look Like Inside a Computer

By Rick Regan January 7th, 2009

A power of two, when expressed as a binary number, is easy to spot: it has one, and only one, 1 bit. For example, 1000, 10, and 0.001 are powers of two. Inside a computer, however, numbers are more generally represented in binary code, not as “pure” binary numbers. As a result, you may not be able to look at the binary representation of a number and tell at a glance whether it’s a power of two or not; it depends on how it’s encoded.

Continue reading “What Powers of Two Look Like Inside a Computer”

The Powers of Two

By Rick Regan November 14th, 2008

The following infinite set of numbers is known as the powers of two:

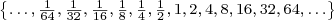$\mbox{\footnotesize{\left\{ {\ldots, \frac{1}{64}, \frac{1}{32}, \frac{1}{16}, \frac{1}{8}, \frac{1}{4}, \frac{1}{2}, 1, 2, 4, 8, 16, 32, 64, \ldots} \right\}}}$ .

Why are they called powers of two? What is the pattern you see? How is the set described mathematically? What are the set’s components? We will answer those questions in this article.

Continue reading “The Powers of Two”

A Standard Definition of The Powers of Two

By Rick Regan November 14th, 2008

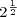What is a power of two exactly? Is 2⁰ a power of two? Is 2^-1 a power of two? How about $\mbox{\footnotesize{2^{\frac{1}{2}}}}$ or $\mbox{\footnotesize{2^{\pi}}}$ ? It depends on how you define it; there are several definitions from which you could choose. Let’s see if we can sort them out and propose a standard definition, or at least a standard definition for our use.

Continue reading “A Standard Definition of The Powers of Two”

Nonstandard Names for The Powers of Two

By Rick Regan November 14th, 2008

Now that you know how the powers of two are named, lets look at other, nonstandard ways to name them. You will see these names on the internet as well as in books. We will not use them on this site other than in this article, and we only discuss them here to make you aware of their use. As a by-product of this discussion, you may gain some insight into the nature of the powers of two. But beware — you may become confused as well!

Continue reading “Nonstandard Names for The Powers of Two”

How to Check If a Number Is a Power of Two

By Rick Regan November 14th, 2008

How can you tell if a number is a power of two?

That’s easy if it’s in the form 2ⁿ, where n is an integer. For example, 2¹², 2⁰, and 2^-37 are powers of two. That is by definition. But what about arbitrary positive numbers like 16,392, 524,288, or 0.00390625? Are they powers of two? Here’s how to tell — if they can be simplified to the form 2ⁿ, they are; if they can’t, they’re not.

Continue reading “How to Check If a Number Is a Power of Two”

Composing Powers of Two Using The Laws of Exponents

By Rick Regan November 14th, 2008

Powers of two can be combined, under the laws of exponents, to create other powers of two. Under these rules, you can multiply powers of two, divide powers of two, or raise a power of two to a power and still get another power of two. You can combine these rules to create complicated expressions, expressions that result in a single power of two. For example,

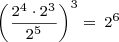$\mbox{\footnotesize{\displaystyle {{\left(\frac{2^4 \cdot 2^3}{2^5}\right)}^3 = \: 2^6}}}$ .

The laws of exponents apply generally to any base; two is no different. But since we’re interested in powers of two, we’ll couch them in terms of powers of two. Once we explain the laws in this way, you’ll understand the math behind the example above.

Continue reading “Composing Powers of Two Using The Laws of Exponents”

A Table of Nonnegative Powers of Two

By Rick Regan November 14th, 2008

Here is a table of the first 65 nonnegative powers of two (from 2⁰ to 2⁶⁴):

Continue reading “A Table of Nonnegative Powers of Two”